【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂生产三种不同型号的电视机,出厂价分别为甲种每台1500元, 乙种每台2100元, 丙种每台2500元, 若商场同时购进其中两种不同型号的电视机共50台,用去9万元.请你通过计算,说明商场有哪些进货方案.
参考答案:
【答案】有两种进货方案:(1)购进甲25台,乙25台;(2)购进甲35台,乙15台。
【解析】
用二元一次方程组解决问题的关键是找到2个合适的等量关系.在本题中可利用“两种型号电视机总数为50”和“计划拨款9万元用于购买电视机”这两个等量关系列方程组解答.
设甲、乙、丙型号的电视机分别为x台,y台,z台.
(1)若选甲、乙,则有:
![]()
解得:![]()
(2)若选甲、丙,则有:
![]()
解得:![]()
(3)若选乙、丙,则有:
![]()
解得:![]() (舍去,不合题意)
(舍去,不合题意)
答:有两种进货方案:(1)购进甲25台,乙25台;(2)购进甲35台,乙15台.
-
科目: 来源: 题型:
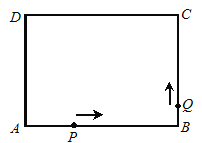
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=3,点P、Q分别从A、B两点出发,按逆时针方向沿矩形的边运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,运动的时间为t秒,当其中某一点到达点A时,运动停止,运动过程中,点P关于直线AQ的对称点记为点M.
(1)点P点在线段AB上运动,点Q在线段BC上运动时,请用含t的式子表示出△APQ的面积S;
(2)当点P在线段BC上运动,且△ABP∽△PCQ时,求t的值;
(3)若点Q在线段CD上,且以A、P、Q、M为顶点的四边形是菱形,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c﹣b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
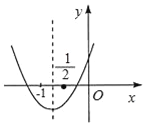
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把抛物线y=
 x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为________.
x2交于点Q,则图中阴影部分的面积为________. 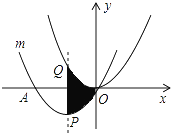
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△BAC中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
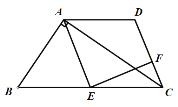
(1)求证:DC=EC.
(2)若AB=6,BC=10,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像与反比例函数
的图像与反比例函数 (k>0)的图像交于点A与点B(a,-4).
(k>0)的图像交于点A与点B(a,-4).

(1)求反比例函数的表达式;
(2)若点P(m,6)是双曲线上的一点,连接OP,过点P作y轴的平行线交直线AB于点C,连接OC,求△POC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市计划购进甲、乙两种商品,已知甲的进价比乙多20元/件,用2000元购进甲种商品的件数与用1600元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价各是多少元?
(2)小丽用950元只购买乙种商品,她购买乙种商品件数y(件),该商品的销售单价x(元),列出y与x函数关系式?若超市销售乙种商品,至少要获得20%的利润,那么小丽最多可以购买多少件乙种商品?
相关试题

