【题目】如图,点A、B、C、D在一条直线上,AB=CD,四边形BECF是平行四边形. 
(1)求证:△AEC≌△DFB;
(2)求证:∠AEB=∠DFC.
参考答案:
【答案】
(1)证明:∵四边形BECF是平行四边形.
∴CE=BF,BE∥CF,BE=CF,
∴∠ACE=∠DBF,
∵AB=CD,
∴AC=DB,
在△AEC和△DFB中,  ,
,
∴△AEC≌△DFB(SAS);
(2)证明:∵△AEC≌△DFB,
∴AE=DF,
在△AEB和△DFC中,  ,
,
∴△AEB≌△DFC(SSS),
∴∠AEB=∠DFC.
【解析】(1)由SAS证明△AEC≌△DFB即可;(2)由由SSS证明△AEB≌△DFC,即可得出结论.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件属于必然事件的是( )
A. 明天我市最高气温为56℃B. 下雨后有彩虹
C. 在1个标准大气压下,水加热到100℃沸腾D. 中秋节晚上能看到月亮
-
科目: 来源: 题型:
查看答案和解析>>【题目】水龙头关闭不严会造成滴水,容器内盛水量w(L)与滴水时间t(h)的关系用可以显示水量的容器做如图1的试验,并根据试验数据绘制出如图2的函数图象,结合图象解答下列问题.
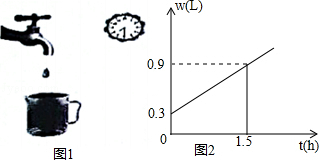
(1)容器内原有水多少升?
(2)求w与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,求证∠B<90°,下面写出了用反证法证明过程中的四个步骤:①所以∠B+∠C+∠A>180°,这与三角形内角和定理相矛盾;②所以∠B<90°;③假设∠B≥90°;④那么由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°.这四个步骤正确的顺序应是_________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中, D , E , F三点分别在AB , AC , BC上,过点D的直线与线段EF的交点为点M , 已知2∠1-∠2=150°,2∠ 2-∠1=30°.
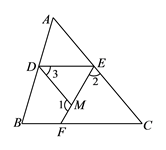
(1)求证:DM∥AC;
(2)若DE∥BC , ∠C =50°,求∠3的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)当PQ的长度取最大值时,PQ与x轴的交点记为D,在x轴上是否存在点E,使以点B,C,E为顶点的三角形与△BQD相似.如果存在,直接写出E点坐标,如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 三角形的正投影一定是三角形B. 长方体的正投影一定是长方形
C. 球的正投影一定是圆D. 圆锥的正投影一定是三角形
相关试题

