【题目】滴滴快车”是一种便捷的出行工具,计价规则如下表:

随着互联网的不断发展,更多的人们选择了“滴滴快车”出行。假设“滴滴快车”的平均行车速度为50 km/h,请回答下列问题:
(1)小明和小冰各自乘坐“滴滴快车”,行车里程分别为3千米和10千米,请问他们各自需付车费多少钱?
(2)张老师与王老师的家和学校在同一条直线上,位置如图所示。一天,张老师和王老师各自从学校“滴滴快车”回家,分别付车费9.6元和24元。请问,张老师和王老师的家相距多少千米?
参考答案:
【答案】(1)小明需付车费8元,小冰需付车费16元;(2)张老师和王老师家相距19.8千米或21千米.
【解析】
(1)根据题意假设行驶距离为a千米,可得车费为1.4a+![]() 元,然后分别将行车里程代入式中即可得解,需要注意的是收费标准中不满8元的按最低消费8元收取,满10元的,给予8折优惠;
元,然后分别将行车里程代入式中即可得解,需要注意的是收费标准中不满8元的按最低消费8元收取,满10元的,给予8折优惠;
(2)分别设张老师家距离学校x千米,王老师家距离学校y千米,注意根据未满10元和满10元分两种情况计算张老师家距离学校的距离,最后将张老师和王老师家距离学校的距离进行相加即可.
(1)根据题意得:小明:3×1.4+![]() ×0.5=6元
×0.5=6元
∵6元<8元
∴小明需付车费8元。
小冰:10×1.4+![]() 元,
元,
20×0.8=16元,
∴小冰需付车费16元.
答:小明需付车费8元,小冰需付车费16元;
(2)设张老师家距离学校x千米,王老师家距离学校y千米.
张老师:①原车费未满10元时:
1.4x+![]()
x=4.8,
②原车费满10元打8折时:
![]() )
)![]()
x=6,
∴张老师家距离学校4.8千米或6千米;
王老师:![]() )
)![]()
y=15,
∴张老师家距离学校15千米,
综上所述:张老师和王老师家为4.8+15=19.8千米或6+15=21千米 .
答:张老师和王老师家相距19.8千米或21千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在一次数学考试中,从某班随机抽取的10名学生得分(单位:分)如下:75,85,90,90,95,85,95,95,100,98.
(1)求这10名学生得分的众数、中位数和平均数;
(2)若该班共有40名学生,估计此次考试的平均成绩约为多少.
-
科目: 来源: 题型:
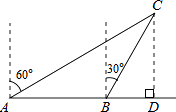
查看答案和解析>>【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知数轴上两点A、B对应的数分别为﹣2、5,点P为数轴上的一动点,其对应的数为x.
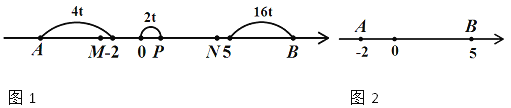
(1)PA= ;PB= (用含x的式子表示)
(2)在数轴上是否存在点P,使PA+PB=10?若存在,请直接写出x的值;若不存在,请说明理由.
(3)如图2,点P以2个单位/s的速度从点O向右运动,同时点A以4个单位/s的速度向左运动,点B以16个单位/s的速度向右运动,在运动过程中,M、N分别是AP、OB的中点,问:
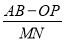 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】湖州市在2017年被评为“全国文明城市”,在评选过程中,湖州市环卫处每天需负责市区范围420千米城市道路的清扫工作,现有环卫工人直接清扫和道路清扫车两种马路清扫方式.已知20名环卫工人和1辆道路清扫车每小时可以清扫20千米马路,30名环卫工人和3辆道路清扫车每小时可以清扫42千米的马路.
(1)1名环卫工人和1辆道路清扫车每小时各能清扫多长的马路?
(2)已知2017年环卫处安排了50名环卫工人参与了直接清扫工作,为保证顺利完成每日的420千米清扫工作,需派出多少辆道路清扫车参与工作(已知2017年环卫工人与清扫车每天工作时间为6小时)?
(3)为了巩固文明城市创建成果,从2018年5月开始,环卫处新增了一辆清扫车参与工作,同时又增加了若干个环卫工人参与直接清扫,使得每日能够较早的完成清扫工作。2018年6月市环卫处扩大清扫范围60千米,同时又增加了20名环卫工人直接参与清扫,此时环卫工人和清扫车每日工作时间仍与5月份相同,那么2018年5月环卫处增加了多少名环卫工人参与直接清扫?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E是AD的中点,延长BC到点F,使CF:BC=1:2,连接DF,EC.若AB=5,AD=8,sinB=
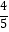 ,则DF的长等于( )
,则DF的长等于( ) 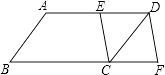
A.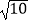
B.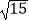
C.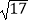
D.2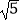
-
科目: 来源: 题型:
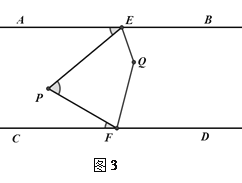
查看答案和解析>>【题目】如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB、CD之间有一动点P,满足0°<∠EPF<180°.



(1)试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?
解:由于点P是平行线AB、CD之间有一动点,因此需要对点P的位置进行分类讨论;如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________。
(2)如图3,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF=_______°.
②猜想∠EPF与∠EQF的数量关系,并说明理由.
③如图4,若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3,此次类推,则∠EPF与∠EQ2018F满足怎样的数量关系?(直接写出结果)
相关试题

