【题目】如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB、CD之间有一动点P,满足0°<∠EPF<180°.


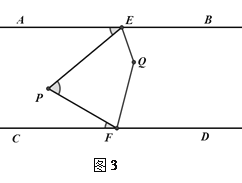

(1)试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?
解:由于点P是平行线AB、CD之间有一动点,因此需要对点P的位置进行分类讨论;如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________。
(2)如图3,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF=_______°.
②猜想∠EPF与∠EQF的数量关系,并说明理由.
③如图4,若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3,此次类推,则∠EPF与∠EQ2018F满足怎样的数量关系?(直接写出结果)
参考答案:
【答案】(1)∠AEP+∠PFC=∠EPF,∠AEP+∠PFC+∠EPF=360°;
(2)①150;
②∠EPF与∠EQF的数量关系为∠EPF+2∠EQF=360°,理由详见解析;
③∠EPF+22019∠EQ2018F=360°.
【解析】
(1)如图1,过点P作PH∥AB,证得 AB∥PH∥CD,然后根据平行线的性质证得结论,如图2,过点P作PH∥AB,证得AB∥PH∥CD ,然后根据平行线的性质证得结论;
(2)①如图3,过点P作PH∥AB,过点Q作QG∥AB,然后根据平行线的性质得到∠EPF=∠AEP+∠CFP,∠EQF=∠BEQ+∠DFQ ,由∠EPF=60°,QE,QF分别平分∠PEB和∠PFD,即可求得结论;
②同①即可得结论;
③由(2)②知∠EPF+2∠EQF=360°,进而∠EPF+22∠EQ1F=360°,
∠EPF+23∠EQ2F=360°,由规律即可求得结论.
(1)如图1,过点P作PH∥AB,
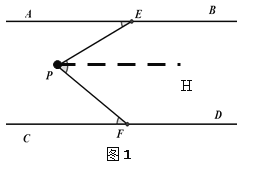
∵AB∥CD,PH∥AB,∴AB∥PH∥CD,
∴∠AEP=∠EPH,∠PFC=∠FPH,
∵∠EPF=∠EPH+∠FPH,
∴∠EPF=∠AEP+∠PFC,
如图2,过点P作PH∥AB,
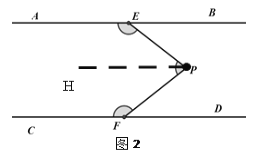
∵AB∥CD,PH∥AB,
∴AB∥PH∥CD,
∴∠AEP+∠EPH=180°,∠CFP+∠FPH=180°,
∵∠EPF=∠EPH+∠FPH,
∴∠AEP+∠PFC+∠EPF=360°.
故答案为∠AEP+∠PFC=∠EPF,∠AEP+∠PFC+∠EPF=360°;
(2)①如图3,过点P作PH∥AB,过点Q作QG∥AB,
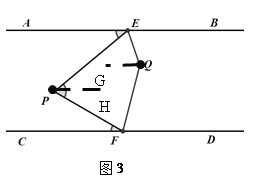
∵AB∥CD,PH∥AB,
∴AB∥PH∥CD,
∴∠AEP=∠EPH,∠PFC=∠FPH,
∵∠EPF=∠EPH+∠FPH,
∴∠EPF=∠AEP+∠PFC,
同理:∠EQF=∠BEQ+∠DFQ,
∵∠EPF=60°,
∴∠AEP+∠PFC=60°,
∴∠BEP+∠DEP=300°,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEQ+∠DFQ=150°,
∴∠EQF=150°;
(2)②∠EPF与∠EQF的数量关系为∠EPF+2∠EQF=360°,
理由:
由(1)和(2)①可知∠EPF+∠BEP+∠DFP=360°,∠EQF=∠BEQ+∠DFQ,
∵QE,QF分别平分∠PEB和∠PFD,
∴∠BEP=2∠BEQ,∠DFP=2∠DFQ,
∴∠BEP+∠DFP=2(∠BEQ+∠DFQ)=2∠EQF,
∴∠EPF+2∠EQF=360°;
(3)由(2)②知∠EPF+2∠EQF=360°,
同理可证:∠EPF+22∠EQ1F=360°,
∠EPF+23∠EQ2F=360°,
……
∠EPF+22019∠EQ2018F=360°,
故答案为∠EPF+22019∠EQ2018F=360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】滴滴快车”是一种便捷的出行工具,计价规则如下表:

随着互联网的不断发展,更多的人们选择了“滴滴快车”出行。假设“滴滴快车”的平均行车速度为50 km/h,请回答下列问题:
(1)小明和小冰各自乘坐“滴滴快车”,行车里程分别为3千米和10千米,请问他们各自需付车费多少钱?
(2)张老师与王老师的家和学校在同一条直线上,位置如图所示。一天,张老师和王老师各自从学校“滴滴快车”回家,分别付车费9.6元和24元。请问,张老师和王老师的家相距多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】湖州市在2017年被评为“全国文明城市”,在评选过程中,湖州市环卫处每天需负责市区范围420千米城市道路的清扫工作,现有环卫工人直接清扫和道路清扫车两种马路清扫方式.已知20名环卫工人和1辆道路清扫车每小时可以清扫20千米马路,30名环卫工人和3辆道路清扫车每小时可以清扫42千米的马路.
(1)1名环卫工人和1辆道路清扫车每小时各能清扫多长的马路?
(2)已知2017年环卫处安排了50名环卫工人参与了直接清扫工作,为保证顺利完成每日的420千米清扫工作,需派出多少辆道路清扫车参与工作(已知2017年环卫工人与清扫车每天工作时间为6小时)?
(3)为了巩固文明城市创建成果,从2018年5月开始,环卫处新增了一辆清扫车参与工作,同时又增加了若干个环卫工人参与直接清扫,使得每日能够较早的完成清扫工作。2018年6月市环卫处扩大清扫范围60千米,同时又增加了20名环卫工人直接参与清扫,此时环卫工人和清扫车每日工作时间仍与5月份相同,那么2018年5月环卫处增加了多少名环卫工人参与直接清扫?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E是AD的中点,延长BC到点F,使CF:BC=1:2,连接DF,EC.若AB=5,AD=8,sinB=
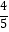 ,则DF的长等于( )
,则DF的长等于( ) 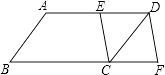
A.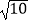
B.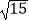
C.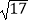
D.2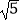
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次主题为“学会生存”的中学生社会实践活动中,春华同学为了锻炼自己,他通过了解市场行情,以每件
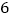 元的价格从批发市场购进若干件印有
元的价格从批发市场购进若干件印有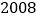 北京奥运标志的文化衫到自由市场去推销,当销售完
北京奥运标志的文化衫到自由市场去推销,当销售完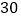 件之后,销售金额达到
件之后,销售金额达到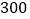 元,余下的每件降价
元,余下的每件降价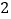 元,很快推销完毕,此时销售金额达到
元,很快推销完毕,此时销售金额达到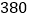 元,春华同学在这次活动中获得纯收入_______元.
元,春华同学在这次活动中获得纯收入_______元. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为( )

A.40cm
B.60cm
C.80cm
D.100cm -
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录的是今年长江某一周内的水位变化情况,这一周的上周末的水位已达到警戒水位
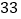 米(正号表示水位比前一天上升,负号表示水位比前一天下降).
米(正号表示水位比前一天上升,负号表示水位比前一天下降). 星期
一
二
三
四
五
六
水位
变化(米)
+0.2
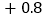
-0.4
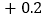
+0.3
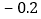
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
相关试题

