【题目】如图,已知等边△ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
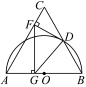
(1)求证:DF是⊙O的切线;
(2)求FG的长;(3)求tan∠FGD的值.
参考答案:
【答案】(1)证明过程见解析;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)连接OD,根据等边三角形得出∠A=∠B=∠C=60°,根据OD=OB得到∠ODB=60°,得到OD∥AC,根据垂直得出切线;(2)根据中位线得出BD=CD=6,根据Rt△CDF的三角函数得出CF的长度,从而得到AF的长度,最后根据Rt△AFG的三角函数求出FG的长度;(3)过点D作DH⊥AB,根据垂直得出FG∥DH,根据Rt△BDH求出BH、DH的长度,然后得出∠GDH的正切值,从而得到∠FGD的正切值.
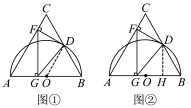
试题解析:(1)如图①,连结OD, ∵△ABC为等边三角形, ∴∠C=∠A=∠B=60°,
而OD=OB, ∴△ODB是等边三角形,∠ODB=60°, ∴∠ODB=∠C,
∴OD∥AC, ∵DF⊥AC,∴OD⊥DF,∴DF是⊙O的切线
(2)∵OD∥AC,点O为AB的中点,∴OD为△ABC的中位线,
∴BD=CD=6.在Rt△CDF中,∠C=60°,∴∠CDF=30°,
∴CF=CD=3,∴AF=AC-CF=12-3=9 在Rt△AFG中,∵∠A=60°,∴FG=AF·sinA=9×=
(3)如图②,过D作DH⊥AB于H.∵FG⊥AB,DH⊥AB,∴FG∥DH,∴∠FGD=∠GDH.在Rt△BDH中,∠B=60°,∴∠BDH=30°,∴BH=BD=3,DH=BH=3.∴tan∠GDH===,
∴tan∠FGD=tan∠GDH=
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点为(4,﹣8),并且经过点(6,﹣4),试确定此抛物线的解析式.并写出对称轴方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-
 .
.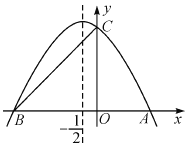
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中既是轴对称图形,又是中心对称图形的是( )
A. 等边三角形 B. 平行四边形 C. 正方形 D. 正五边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=3(x-a)2的图象上,当x>2时,y随x的增大而增大,则a的取值范围是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(-4,y1),B(-3,y2),C(3,y3)三点都在二次函数y=-2(x+2)2的图象上,则y1,y2,y3的大小关系为___.
相关试题

