【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
参考答案:
【答案】(1)等腰三角形;理由见解析;(2)直角三角形;理由见解析;(3) ![]() =0,
=0, ![]() =-1
=-1
【解析】试题分析:(1)、将x=-1代入方程得出a+c﹣2b+a﹣c=0。从而得出结论;(2)、根据方程有两个相等的实数根,则根的判别式为零,从而得出答案;(3)、将a=b=c代入,从而得出2ax2+2ax=0即x2+x=0,然后求出方程的解.
试题解析:(1)、△ABC是等腰三角形;
理由:∵x=﹣1是方程的根, ∴(a+c)×(﹣1)2﹣2b+(a﹣c)=0,∴a+c﹣2b+a﹣c=0,
∴a﹣b=0,∴a=b, ∴△ABC是等腰三角形;
(2)、∵方程有两个相等的实数根,∴(2b)2﹣4(a+c)(a﹣c)=0,
∴4b2﹣4a2+4c2=0,∴a2=b2+c2, ∴△ABC是直角三角形;
(3)、当△ABC是等边三角形,∴(a+c)x2+2bx+(a﹣c)=0,可整理为:
2ax2+2ax=0,∴x2+x=0,解得:x1=0,x2=﹣1
-
科目: 来源: 题型:
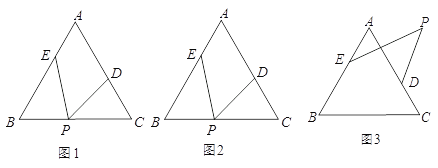
查看答案和解析>>【题目】△ABC中,∠A=60°,点D、E分别是△ABC边AC、AB上的点(不与A、B、C重合),点P是一动点,令∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边BC上,如图l,且∠α=50°,则∠1+∠2= °.
(2)若点P在边BC上运动,如图2,试判断∠α、∠1、∠2之间的关系,并证明.
(3)直接写出:若点P运动到△ABC形外,如图3,则∠α、∠l、∠2之间的关系为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系XOY中,有A(3 , 2) ,B (-1 ,-4 ),P是X轴上的一点,Q是Y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别是(﹣3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.

(1)当点C运动到线段OB的中点时,求t的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;
(3)在线段PE上取点F,使PF=2,过点F作MN⊥PE,截取FM=
 ,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值.
,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若∠AOB=70°,过点O作射线OC,∠AOC=30°,则∠COB=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣2x+1向下平移2个单位,再向左平移1个单位,所得抛物线的解析式是( )
A. y=x2﹣2x﹣1 B. y=x2+2x﹣1 C. y=x2﹣2 D. y=x2+2
相关试题

