【题目】已知:如图,∠B=∠C,BD=CE,AB=DC,
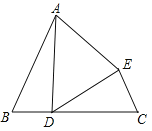
①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.
参考答案:
【答案】①见解析;②见解析.
【解析】
①先根据∠B=∠C,BD=CE,AB=DC,判定△ABD≌DCE,得出DA=DE,进而得到△ADE为等腰三角形;
②根据△ABD≌△DCE,得出∠BAD=∠CDE,再根据三角形内角和定理和平角的定义,得到∠ADE=60°,最后可判定等腰△ADE为等边三角形.
①在△ABD和△DCE中,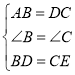 ,
,
∴△ABD≌△DCE(SAS),
∴DA=DE,
即△ADE为等腰三角形
②∵△ABD≌△DCE,
∴∠BAD=∠CDE,
∵∠B=60°,
∴∠BAD+∠ADB=120°,
∴∠CDE+∠ADB=120°,
∴∠ADE=60°,
又∵△ADE为等腰三角形,
∴△ADE为等边三角形.
-
科目: 来源: 题型:
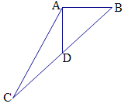
查看答案和解析>>【题目】如图,在△ABC中,AB=6,AC=10,BC边上的中线AD=4,则△ABC的面积为___________;
-
科目: 来源: 题型:
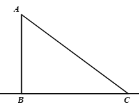
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=3,BC=4,AC=5,在直线BC上有P点,使△PAC是以AC为腰的等腰三角形,则BP的长为____________.
-
科目: 来源: 题型:
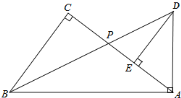
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过D作DE⊥AC于E,AB-BC=4,AC=8,则△ABP面积为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,笔直的公路上有A、B两个站点相距40km,在公路的同侧有C、D两个村庄,DA⊥AB,CB⊥AB,且DA=20km,CB=10km,现政府决定在A、B之间建一个土特产加工基地E.
(1)若要使土特产加工基地E点到C、D两村的距离相等,请用直尺和圆规在图1中作出点E;
(2)在(1)的条件下求出基地E到A站的距离;
(3)若要使土特产加工基地E点到C、D两村的距离和(即DE +EC)最小,求出此最小的距离和.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
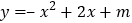 的图象如图所示,则关于
的图象如图所示,则关于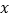 的一元二次方程
的一元二次方程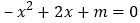 的根为________;不等式
的根为________;不等式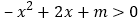 的解集是________;当
的解集是________;当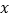 ________时,
________时,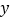 随
随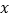 的增大而减小.
的增大而减小.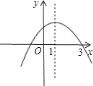
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,Rt△ABC和Rt△ABD中,∠ACB=∠ADB=90°,E为AB中点.
(1)若两个直角三角形的直角顶点在AB的异侧(如图1),连接CD,取CD中点F,连接EF、DE、CE,则DE与CE数量关系为 ,EF与CD位置关系为 ;
(2)若两个直角三角形的直角顶点在AB的同侧(如图2),连接CD、DE、CE.
①若∠CAB=25°,∠DBA=35°,判断△DEC的形状,并说明理由;
②若∠CAB+∠DBA=
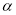 ,当
,当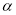 为多少度时,△DEC为等腰直角三角形,并说明理由.
为多少度时,△DEC为等腰直角三角形,并说明理由.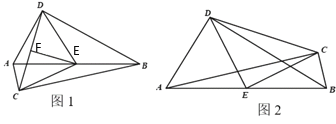
相关试题

