【题目】在数学课上,老师提出如下问题:已知:线段a,b(如图1).
求作:等腰△ABC,使AB=AC,BC=a,BC边上的高为b.
小姗的作法如下:如图2,
(i)作线段BC=a;
(ii)作线段BC的垂直平分线MN交线段BC于点D;
(iii)在MN上截取线段DA=b,连接AB,AC.所以,△ABC就是所求作的等腰三角形.
老师说:“小姗的作法正确”.
请回答:得到△ABC是等腰三角形的依据是: .
参考答案:
【答案】垂直平分线上的点到线段两个端点距离相等;有两条边相等的三角形是等腰三角形
【解析】解:由作法得MN垂直平分BC,则AB=AC.
所以答案是垂直平分线上的点到线段两个端点距离相等;有两条边相等的三角形是等腰三角形.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,若P,Q为某个菱形相邻的两个顶点,且该菱形的两条对角线分别与x轴,y轴平行,则称该菱形为点P,Q的“相关菱形”.图1为点P,Q的“相关菱形”的一个示意图.

已知点A的坐标为(1,4),点B的坐标为(b,0),
(1)若b=3,则R(﹣1,0),S(5,4),T(6,4)中能够成为点A,B的“相关菱形”顶点的是;
(2)若点A,B的“相关菱形”为正方形,求b的值;
(3)⊙B的半径为 ,点C的坐标为(2,4).若⊙B上存在点M,在线段AC上存在点N,使点M,N的“相关菱形”为正方形,请直接写出b的取值范围.
,点C的坐标为(2,4).若⊙B上存在点M,在线段AC上存在点N,使点M,N的“相关菱形”为正方形,请直接写出b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )

A.7.2 cm
B.5.4 cm
C.3.6 cm
D.0.6 cm -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来由于空气质量的变化,以及人们对自身健康的关注程度不断提高,空气净化器成为很多家庭的新电器.某品牌的空气净化器厂家为进一步了解市场,制定生产计划,根据2016年下半年销售情况绘制了如下统计图,其中同比增长率=(
 ﹣1)×100%,下面有四个推断:
﹣1)×100%,下面有四个推断:
①2016年下半年各月销售量均比2015年同月销售量增多
②第四季度销售量占下半年销售量的七成以上
③下半年月均销售量约为16万台
④下半年月销售量的中位数不超过10万台
其中合理的是( )
A.①②
B.①④
C.②③
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A. 2,
 B. 2,1 C. 4,
B. 2,1 C. 4, D. 4,3
D. 4,3 -
科目: 来源: 题型:
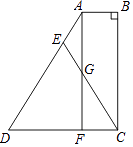
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且AB=FC,E为AD上一点,EC交AF于点G,EA=EG. 求证:ED=EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解方程组的部分过程,回答下列问题
解方程组

现有两位同学的解法如下:
解法一;由①,得x=2y+5,③
把③代入②,得3(2y+5)﹣2y=3.……
解法二:①﹣②,得﹣2x=2.……
(1)解法一使用的具体方法是________,解法二使用的具体方法是______,以上两种方法的共同点是________.
(2)请你任选一种解法,把完整的解题过程写出来
相关试题

