【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且AB=FC,E为AD上一点,EC交AF于点G,EA=EG. 求证:ED=EC.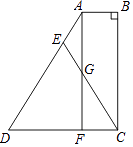
参考答案:
【答案】解:证明:∵AB∥DC,FC=AB, ∴四边形ABCF是平行四边形.
∵∠B=90°,
∴四边形ABCF是矩形.
∴∠AFC=90°,
∴∠D=90°﹣∠DAF,∠ECD=90°﹣∠CGF.
∵EA=EG,
∴∠EAG=∠EGA.
∵∠EGA=∠CGF,
∴∠DAF=∠CGF.
∴∠D=∠ECD.
∴ED=EC
【解析】先证明四边形ABCF是平行四边形.再证出四边形ABCF是矩形.得出∠AFC=90°,得出∠D=90°﹣∠DAF,∠ECD=90°﹣∠CGF.由等腰三角形的性质得出∠EAG=∠EGA.由对顶角相等得出∠DAF=∠CGF.证出∠D=∠ECD.即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来由于空气质量的变化,以及人们对自身健康的关注程度不断提高,空气净化器成为很多家庭的新电器.某品牌的空气净化器厂家为进一步了解市场,制定生产计划,根据2016年下半年销售情况绘制了如下统计图,其中同比增长率=(
 ﹣1)×100%,下面有四个推断:
﹣1)×100%,下面有四个推断:
①2016年下半年各月销售量均比2015年同月销售量增多
②第四季度销售量占下半年销售量的七成以上
③下半年月均销售量约为16万台
④下半年月销售量的中位数不超过10万台
其中合理的是( )
A.①②
B.①④
C.②③
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:已知:线段a,b(如图1).

求作:等腰△ABC,使AB=AC,BC=a,BC边上的高为b.
小姗的作法如下:如图2,
(i)作线段BC=a;
(ii)作线段BC的垂直平分线MN交线段BC于点D;
(iii)在MN上截取线段DA=b,连接AB,AC.所以,△ABC就是所求作的等腰三角形.
老师说:“小姗的作法正确”.
请回答:得到△ABC是等腰三角形的依据是: . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A. 2,
 B. 2,1 C. 4,
B. 2,1 C. 4, D. 4,3
D. 4,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解方程组的部分过程,回答下列问题
解方程组

现有两位同学的解法如下:
解法一;由①,得x=2y+5,③
把③代入②,得3(2y+5)﹣2y=3.……
解法二:①﹣②,得﹣2x=2.……
(1)解法一使用的具体方法是________,解法二使用的具体方法是______,以上两种方法的共同点是________.
(2)请你任选一种解法,把完整的解题过程写出来
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程3x2﹣kx+k﹣4=0.
(1)判断方程根的情况;
(2)若此方程有一个整数根,请选择一个合适的k值,并求出此时方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组自然数1,2,3…k,去掉其中一个数后剩下的数的平均数为16,则去掉的数是________.
相关试题

