【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
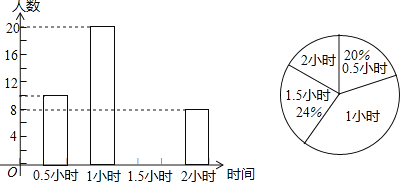
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)求表示户外活动时间1小时的扇形圆心角的度数;
(4)本次调查中学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数是多少?
参考答案:
【答案】(1)50(人);(2)12(人);见解析(3)144°;(4)平均活动时间符合上级要求;户外活动时间的众数和中位数均为1小时.
【解析】
试题分析:(1)由总数=某组频数÷频率计算;
(2)户外活动时间为1.5小时的人数=总数×24%;
(3)扇形圆心角的度数=360×比例;
(4)计算出平均时间后分析.
解:(1)调查人数=10÷20%=50(人);
(2)户外活动时间为1.5小时的人数=50×24%=12(人);
补全频数分布直方图;
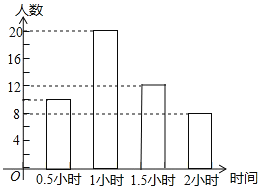
(3)表示户外活动时间1小时的扇形圆心角的度数=![]() ×360°=144°;
×360°=144°;
(4)户外活动的平均时间=![]() (小时),
(小时),
∵1.18>1,
∴平均活动时间符合上级要求;
户外活动时间的众数和中位数均为1小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a2+b2)(a2+b2﹣2)=3,则a2+b2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2﹣2x﹣1的值为2,则3x2﹣6x的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD与等边△AEF的边长相等,且E、F分别在BC、CD,则∠BAD的度数是( )
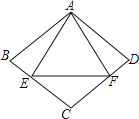
A.80° B.90° C.100° D.120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(﹣8,0),直线BC经过点B(﹣8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′,此时边OA′与边BC交于点P,边B′C′与BC的延长线交于点Q,连接AP.
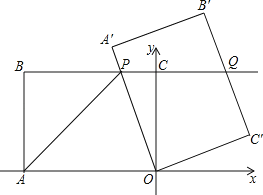
(1)四边形OABC的形状是 .
(2)在旋转过程中,当∠PAO=∠POA,求P点坐标.
(3)在旋转过程中,当P为线段BQ中点时,连接OQ,求△OPQ的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).有下列结论:
①abc>0;
②4a﹣2b+c<0;
③4a+b=0;
④抛物线与x轴的另一个交点是(5,0);
⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是( )
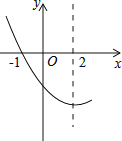
A.①②③ B.②④⑤ C.①③④ D.③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,管中放置着三根同样的绳子AA1、BB1、CC1.小明在左侧选两个打一个结,小红在右侧选两个打一个结,则这三根绳子能连结成一根长绳的概率为 .

相关试题

