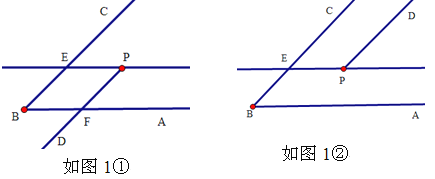
【题目】(1)如图1,P是∠ABC内一点,请过点P画射线PD,使PD∥BC;过点P画直线PE∥BA,交BC于点E.请画图并通过观察思考后你发现∠ABC与∠DPE的大小关系是 ,并说明理由.
(2)如图2,直线a,b所成的角跑到画板外面去了,为了测量这两条直线所成的角的度数,请画图并简单地写出你的方法.

参考答案:
【答案】(1)相等或互补 (2)见解析
【解析】试题分析:(1)分两种情况讨论;(2)利用平行线的性质或三角形的内角和设计方法.
试题解析:(1)相等或互补
理由如下:
如图1①,
DP交AB于点F.
∵PD∥BC,
∴∠ABC=∠AFP,
∵PE∥BA,
∴∠AFP=∠DPE,
∴∠ABC=∠DPE;
如图1②,
设DP交AB于点F.
∵PD∥BC,
∴∠ABC=∠CEP,
∵PD∥BC,
∴∠CEP+∠DPE=180°,
∴∠ABC+∠DPE=180°;
(2)方法一:
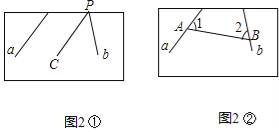
如图2①,设直线b与木板交于点P,
过点P作PC∥a,量出直线b与PC的夹角度数,即为直线a,b所成角的度数,
依据是:两直线平行,同位角相等;
方法二:
如图2②,在直线a,b上各取一点A,B,
连结AB,测得∠1,∠2的度数,
则180°﹣∠1﹣∠2即为直线a,b所成角的度数;
依据是:三角形内角和为180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣4x+m的顶点在x轴上,则m的值等于( )
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,十位数字与个位数字之和为5,符合条件的数有_______个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类.在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,表)和图是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
各种图书
频数
频率
自然科学
400
0.20
文学艺术
1000
0.50
社会百科
m
0.25
哲学
n
(1)表中m= ,n= ;
(2)在图中,将表示“自然科学”的部分补充完整;
(3)若该学校打算采购一万册图书,请你估算“哲学”类图书应采购多少册较合适?
(4)根据图表提供的信息,请你提出一条合理化的建议.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.
(1)求二次函数
 的解析式;
的解析式;(2)将
 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线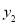 ,直线y=m(m>0)交
,直线y=m(m>0)交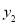 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);(3)在(2)的条件下,
 、
、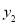 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与 、
、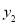 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与 、
、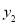 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,解答下面的问题:
我们知道方程
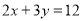 有无数个解,但在实际问题中往往只需求出其正整数解.
有无数个解,但在实际问题中往往只需求出其正整数解.例:由
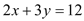 ,得:
,得: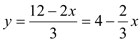 (
( 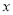 、
、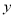 为正整数).要使
为正整数).要使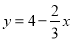 为正整数,则
为正整数,则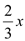 为正整数,可知:
为正整数,可知: 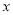 为3的倍数,从而
为3的倍数,从而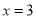 ,代入
,代入 .所以
.所以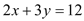 的正整数解为
的正整数解为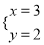 .
. 问题:
(1)请你直接写出方程
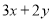 =8的正整数解 .
=8的正整数解 .(2)若
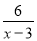 为自然数,则满足条件的正整数
为自然数,则满足条件的正整数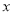 的值有( )
的值有( )A.3个 B.4个 C.5个 D.6个
(3)关于
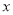 ,
, 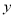 的二元一次方程组
的二元一次方程组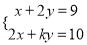 的解是正整数,求整数
的解是正整数,求整数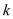 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程
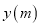 和所经过的时间
和所经过的时间 之间的函数图像如图所示,则下列说法不正确的是( )
之间的函数图像如图所示,则下列说法不正确的是( )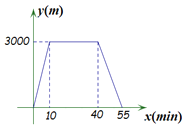
A.娟娟同学与超市相距
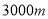
B.娟娟同学去超市途中的速度是
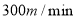
C.娟娟同学在超市逗留了
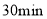
D.娟娟同学从超市返回家比从家里去超市的速度快
相关试题

