【题目】如图,点D在BC上,AB=AC=BD,AD=DC,则∠BAC的度数是 .

参考答案:
【答案】108°
【解析】
试题分析:先设∠C=x,由AB=AC可知,∠B=x,由AD=DC可知∠C=∠DAC=x,由三角形外角的性质可知∠ADB=∠C+∠DAC=2x,根据AB=BD可知∠ADB=∠BAD=2x,再在△ABD中,由三角形内角和定理即可得出关于x的一元一次方程,求出x的值即可,然后根据三角形的内角和即可得到结论.
解:设∠C=x,
∵AB=AC,
∴∠C=∠B=x,
∵AD=DC,
∴∠C=∠DAC=x,
∴∠ADB=∠C+∠DAC=2x,
∵AB=BD,
∴∠ADB=∠BAD=2x,
在△ABD中,∠B=x,∠ADB=∠BAD=2x,
∴x+2x+2x=180°,
解得x=36°.
∴∠C=36°,
∴∠BAC=108°,
故答案为:108°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一条边长为6,另一边长为13,则它的周长为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:|﹣5|+(﹣3)2﹣(π﹣3.14)0×(﹣
 )﹣2÷(﹣2)2017
)﹣2÷(﹣2)2017(2)先化简,再求值:[b(a﹣3b)﹣a(3a+2b)+(3a﹣b)(2a﹣3b)]÷(﹣3a),其中a,b满足2a﹣8b﹣5=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC,BD交于O点,且AB
 CD,那么图中的全等三角形有( )
CD,那么图中的全等三角形有( )
A.2对 B.3对 C.4对 D.5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
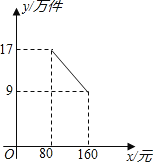
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.
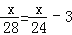
B.
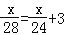
C.
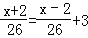
D.
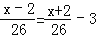
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点.
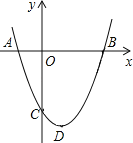
(1)求该抛物线的函数关系式;
(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD,请求出P点的坐标.
相关试题

