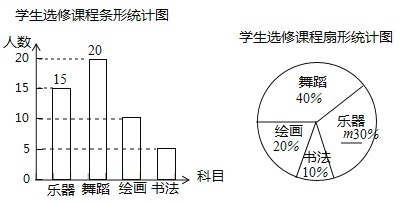
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
参考答案:
【答案】(1)本次调查的学生共有50人,在扇形统计图中,m的值是30%;(2)图见解析;(3)![]() .
.
【解析】
试题分析:(1)用选舞蹈课的人数除以它占本次调查的学生总人数的百分率,求出本次调查的学生人数;然后用选乐器课的人数除以本次调查的学生总人数,求出在扇形统计图中m的值;(2)用本次调查的学生总人数乘参加绘画课、书法课的人数占总人数的百分率,求出参加绘画课、书法课的人数;然后根据参加绘画课、书法课的人数,将条形统计图补充完整即可;(3)判断出在被调查的学生中,选修书法的有3名男同学,2名女同学,然后应用列表法,写出所抽取的2名同学恰好是1名男同学和1名女同学的概率即可.
试题解析:(1)20÷40%=50(人)
15÷50=30%
答:本次调查的学生共有50人,在扇形统计图中,m的值是30%.
(2)50×20%=10(人)
50×10%=5(人)
 .
.
(3)∵5﹣2=3(名),
∴选修书法的5名同学中,有3名男同学,2名女同学,
男 | 男 | 男 | 女 | 女 | |
男 | / | (男,男) | (男,男) | (男,女) | (男,女) |
男 | (男,男) | / | (男,男) | (男,女) | (男,女) |
男 | (男,男) | (男,男) | / | (男,女) | (男,女) |
女 | (女,男) | (女,男) | (女,男) | / | (女,女) |
女 | (女,男) | (女,男) | (女,男) | (女,女) | / |
所有等可能的情况有20种,所抽取的2名同学恰好是1名男同学和1名女同学的情况有12种,
则P(一男一女)=![]() =
=![]()
答:所抽取的2名同学恰好是1名男同学和1名女同学的概率是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简、在求值:
(1)(4a2-3a)-(1-4a+4a2),其中a=-2
(2)有8个算式,排成4行2列
2+2,2×2
3+
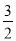 ,3×
,3×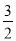
4+
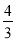 ,4×
,4×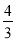
5+
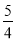 ,5×
,5×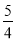
①同一行中两个算式的结果怎样?
②算式2019+
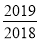 和2019×
和2019×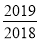 的结果相等吗?
的结果相等吗?③请你写出算式,试一试,再探索其规律,用含自然数n的代数式表示这一规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
A. △ABD与△ABC的周长相等
B. △ABD与△ABC的面积相等
C. 菱形的周长等于两条对角线之和的两倍
D. 菱形的面积等于两条对角线之积的两倍
-
科目: 来源: 题型:
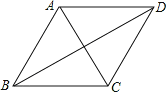
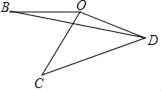
查看答案和解析>>【题目】将线段OB绕点O逆时针旋转60°得到线段OC,继续旋转α(0°<α<120°)得到线段OD,连接CD.
(1)如图,连接BD,则∠BDC的大小=_____(度);
(2)将线段OB放在平面直角坐标系中,O是坐标原点,点B的坐标为(﹣6,0),以OB为斜边作Rt△OBE,使∠OBE=∠OCD,且点E在第三象限,若∠CED=90°,则α的大小=_____(度),点D的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】江南新校区建设需运送3×105立方米的土石方,闽北运输公司承担了该项工程的运送任务.
(1)写出完成运送任务所需的时间y(单位:天)与公司平均每天的运送量x(单位:立方米/天)之间的关系式是 ;
(2)如果公司平均每天的运送量比原计划提高20%,按这个进度公司可以比规定时间提前10天完成运送任务,那么公司平均每天的运送量x是多少?
(3)实际运送时,公司派出80辆车,每辆车按问题(2)中提高后的运送量运输,若先运送了25天,后来由于工程进度的需要,剩下的任务须在20天内完成,那么公司至少要增加多少辆同样型号的车才能按时完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E.过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为8,∠CDF=22.5°,求阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天)
1≤x<9
9≤x<15
x≥15
售价(元/斤)
第1次降价后的价格
第2次降价后的价格
销量(斤)
80﹣3x
120﹣x
储存和损耗费用(元)
40+3x
3x2﹣64x+400
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
相关试题

