【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).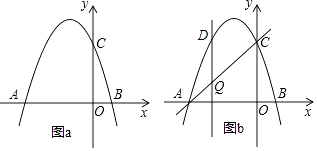
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4S△BOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
参考答案:
【答案】
(1)解:把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得
![]() ,
,
解得 ![]() .
.
故该抛物线的解析式为:y=﹣x2﹣2x+3.
(2)解:由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).
∵S△AOP=4S△BOC,
∴ ![]() ×3×|﹣x2﹣2x+3|=4×
×3×|﹣x2﹣2x+3|=4× ![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x﹣7=0,
解得x=﹣1或x=﹣1±2 ![]() .
.
则符合条件的点P的坐标为:(﹣1,4)或(﹣1+2 ![]() ,﹣4)或(﹣1﹣2
,﹣4)或(﹣1﹣2 ![]() ,﹣4)
,﹣4)
(3)解:设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,
得 ![]() ,
,
解得 ![]() .
.
即直线AC的解析式为y=x+3.
设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),
QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+ ![]() )2+
)2+ ![]() ,
,
∴当x=﹣ ![]() 时,QD有最大值
时,QD有最大值 ![]()
【解析】(1)利用待定系数法,把点A、C的坐标分别代入函数解析式,列出方程组,求解即可求出抛物线的解析式。
(2)设P点坐标为(x,-x2-2x+3),根据S△AOP=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
(3)先运用待定系数法求出直线AC的解析式,再设Q点坐标为(x,x+3),则D点坐标为(x,x2+2x-3),然后求出QD与x的函数解析式,求出其顶点坐标,即可求出线段QD长度的最大值。
【考点精析】通过灵活运用公式法和确定一次函数的表达式,掌握要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.

(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B,C分别在AD,AF上,此时BD=CF,BD⊥CF成立.
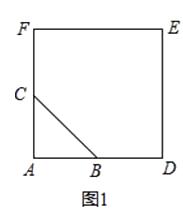
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交AF,CF于点N,H.
①求证:BD⊥CF;
②当AB=2,AD=3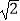 时,求线段AN的长.
时,求线段AN的长.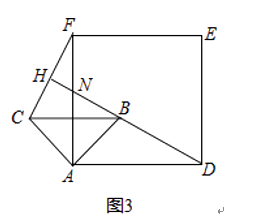
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系中,两个量之间为反比例函数关系的是( )
A.正方形的面积S与边长a的关系
B.正方形的周长L与边长a的关系
C.长方形的长为a,宽为20,其面积S与a的关系
D.长方形的面积为40,长为a,宽为b,a与b的关系 -
科目: 来源: 题型:
查看答案和解析>>【题目】y是x的反比例函数,下表给出了x与y的一些值:
x
﹣2
﹣1
﹣


1
3
y

2
﹣1
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的反比例函数,且x=8时,y=12.
(1)写出y与x之间的函数关系式;
(2)如果自变量x的取值范围是2≤x≤3,求y的取值范围.
相关试题

