Question

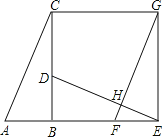
【题目】如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．

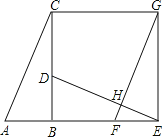
（1）判断线段DE、FG的位置关系，并说明理由；

（2）连结CG，求证：四边形CBEG是正方形．

Answer 1

【答案】（1）FG⊥ED；（2）见解析

【解析】

试题分析：（1）根据旋转和平移可得∠DEB=∠ACB，∠GFE=∠A，再根据∠ABC=90°可得∠A+∠ACB=90°，进而得到∠DEB+∠GFE=90°，从而得到DE、FG的位置关系是垂直；

（2）根据旋转和平移找出对应线段和角，然后再证明是矩形，后根据邻边相等可得四边形CBEG是正方形．

（1）解：FG⊥ED．理由如下：

∵△ABC绕点B顺时针旋转90°至△DBE后，

∴∠DEB=∠ACB，

∵把△ABC沿射线平移至△FEG，

∴∠GFE=∠A，

∵∠ABC=90°，

∴∠A+∠ACB=90°，

∴∠DEB+∠GFE=90°，

∴∠FHE=90°，

∴FG⊥ED；

（2）证明：根据旋转和平移可得∠GEF=90°，∠CBE=90°，CG∥EB，CB=BE，

∵CG∥EB，

∴∠BCG=∠CBE=90°，

∴四边形BCGE是矩形，

∵CB=BE，

∴四边形CBEG是正方形．