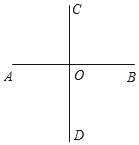
【题目】操作:如图,直线AB与CD交于点O,按要求完成下列问题.
(1)用量角器量得∠AOC= 度.AB与CD的关系可记作 .
(2)画出∠BOC的角平分线OM,∠BOM=∠ = 度.
(3)在射线OM上取一点P,画出点P到直线AB的距离PE.
(4)如图若按“上北下南左西右东”的方位标记,请画出表示“南偏西30°”的射线OF.
参考答案:
【答案】(1)90,AB⊥CD;(2)COM,45;(3)见解析;(4)见解析.
【解析】
(1)运用量角器测量,即可得到结论;
(2)画出∠BOC的角平分线OM,利用角平分线的定义,即可得到结论;
(3)在射线OM上取一点P,过点P作直线AB的垂线PE.
(4)依据“南偏西30°”即可得到射线OF.
(1)用量角器量得∠AOC=90°,AB与CD的关系可记作 AB⊥CD.
故答案为:90,AB⊥CD;
(2)如图所示,OM即为所求,∠BOM=∠COM=45°.
故答案为:COM,45;
(3)如图所示,PE即为所求;
(4)如图所示,OF即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内,如图,在ABCD中,AB=10,AD=15,tanA=
 ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.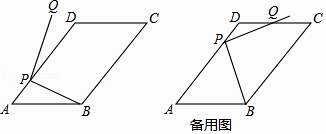
(1)当∠DPQ=10°时,求∠APB的大小;
(2)当tan∠ABP:tanA=3:2时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′.则线段B′C= .
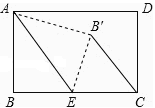
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0,每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12),符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据.
月份n(月)
1
2
成本y(万元/件)
11
12
需求量x(件/月)
120
100
(1)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b被c所截,则∠1与∠2是( )
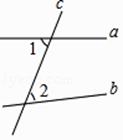
A.同位角
B.内错角
C.同旁内角
D.邻补角 -
科目: 来源: 题型:
查看答案和解析>>【题目】某开发公司生产的960件新产品,需要精加工后,才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元。
(1)求甲、乙两个工厂每天各能加工多少件新产品。
(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成。在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费。 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
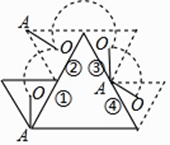
A.240°
B.360°
C.480°
D.540°
相关试题

