【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0,每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12),符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据.
月份n(月) | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.
参考答案:
【答案】
(1)解:由题意,设y=a+ ![]() ,
,
由表中数据可得:  ,解得:
,解得: ![]() ,
,
∴y=6+ ![]() ,
,
由题意,若12=18﹣(6+ ![]() ),则
),则 ![]() =0,
=0,
∵x>0,
∴ ![]() >0,
>0,
∴不可能
(2)解:将n=1、x=120代入x=2n2﹣2kn+9(k+3),得:120=2﹣2k+9k+27,
解得:k=13,
∴x=2n2﹣26n+144,
将n=2、x=100代入x=2n2﹣26n+144也符合,
∴k=13;
由题意,得:18=6+ ![]() ,
,
解得:x=50,
∴50=2n2﹣26n+144,即n2﹣13n+47=0,
∵△=(﹣13)2﹣4×1×47<0,
∴方程无实数根,
∴不存在
(3)解:第m个月的利润为W,
W=x(18﹣y)=18x﹣x(6+ ![]() )
)
=12(x﹣50)
=24(m2﹣13m+47),
∴第(m+1)个月的利润为W′=24[(m+1)2﹣13(m+1)+47]=24(m2﹣11m+35),
若W≥W′,W﹣W′=48(6﹣m),m取最小1,W﹣W′取得最大值240;
若W<W′,W﹣W′=48(m﹣6),由m+1≤12知m取最大11,W﹣W′取得最大值240;
∴m=1或11
【解析】(1)设y=a+ ![]() ,将表中相关数据代入可求得a、b,根据12=18﹣(6+
,将表中相关数据代入可求得a、b,根据12=18﹣(6+ ![]() ),则
),则 ![]() =0可作出判断;(2)将n=1、x=120代入x=2n2﹣2kn+9(k+3)可求得k的值,先由18=6+
=0可作出判断;(2)将n=1、x=120代入x=2n2﹣2kn+9(k+3)可求得k的值,先由18=6+ ![]() 求得x=50,根据50=2n2﹣26n+144可判断;(3)第m个月的利润W=x(18﹣y)=18x﹣x(6+
求得x=50,根据50=2n2﹣26n+144可判断;(3)第m个月的利润W=x(18﹣y)=18x﹣x(6+ ![]() )=24(m2﹣13m+47),第(m+1)个月的利润为W′=24[(m+1)2﹣13(m+1)+47]=24(m2﹣11m+35),分情况作差结合m的范围,由一次函数性质可得.
)=24(m2﹣13m+47),第(m+1)个月的利润为W′=24[(m+1)2﹣13(m+1)+47]=24(m2﹣11m+35),分情况作差结合m的范围,由一次函数性质可得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的对角线相交于O,给出下列 5个条件:①AB∥CD ;②AD∥BC;③AB=CD ;④∠BAD=∠BCD;⑤OA=OC.从以上5个条件中任选 2个条件为一组,能推出四边形ABCD为平行四边形的有( )
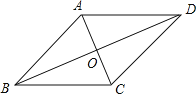
A. 4组 B. 5组 C. 6组 D. 7组
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内,如图,在ABCD中,AB=10,AD=15,tanA=
 ,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.
,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.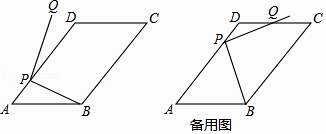
(1)当∠DPQ=10°时,求∠APB的大小;
(2)当tan∠ABP:tanA=3:2时,求点Q与点B间的距离(结果保留根号);
(3)若点Q恰好落在ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′.则线段B′C= .
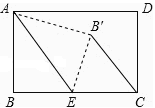
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作:如图,直线AB与CD交于点O,按要求完成下列问题.
(1)用量角器量得∠AOC= 度.AB与CD的关系可记作 .
(2)画出∠BOC的角平分线OM,∠BOM=∠ = 度.
(3)在射线OM上取一点P,画出点P到直线AB的距离PE.
(4)如图若按“上北下南左西右东”的方位标记,请画出表示“南偏西30°”的射线OF.
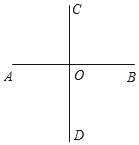
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b被c所截,则∠1与∠2是( )
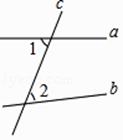
A.同位角
B.内错角
C.同旁内角
D.邻补角 -
科目: 来源: 题型:
查看答案和解析>>【题目】某开发公司生产的960件新产品,需要精加工后,才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元。
(1)求甲、乙两个工厂每天各能加工多少件新产品。
(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成。在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费。 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由。
相关试题

