【题目】如图,点D在AC上,点E在AB上,且AB=AC,BD=BC,AD=DE=BE.求∠A的度数. 
参考答案:
【答案】解:设∠A=x°,
∵AD=DE=BE,
∴∠ABD=∠BDE,∠A=∠AED,
由三角形的外角性质得,∠AED=∠ABD+∠BDE=2∠ABD,
∴∠ABD= ![]() x°,
x°,
在△ABD中,∠BDC=∠A+∠ABD=x°+ ![]() x°=
x°= ![]() x°,
x°,
∵BD=BC,
∴C=∠BDC,
∵AB=AC,
∴∠C=∠ABC,
∴∠ABC=∠C=∠BDC= ![]() x°,
x°,
在△ABC中,由三角形内角和定理得,
x+ ![]() x+
x+ ![]() x=180,
x=180,
解得x=45,
所以,∠A=45°.
【解析】设∠A=x°,根据等边对等角和三角形的一个外角等于与它不相邻的两个内角的和表示出∠ABD,再表示出∠BDC,根据等边对等角可得∠C=∠BDC,∠C=∠ABC,然后利用三角形的内角和等于180°列方程求解即可.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣2x2+4x+3的图象的顶点坐标是( )
A. (1,5)B. (﹣1,5)C. (1,3)D. (﹣1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:在四边形ABCD(图2)中,取对角线BD的中点O,连接OA、OC.得折线AOC,再过点O作OE∥AC交CD于E,则直线AE即为四边形ABCD的一条“好线”.
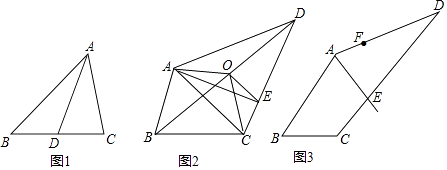
(1)如图(1),试说明中线AD平分△ABC的面积;
(2)如图(2),请你探究四边形ABCO的面积和四边形ABCD面积的关系,并说明理由;
(3)解:在图(2)中,请你说明直线AE是四边形ABCD的一条“好线”;
(4)如图(3),若AE为一条“好线”,F为AD边上的一点,请作出四边形ABCD经过F点的“好线”,并对你的画图作适当说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(﹣2,3)向右平移3个单位长度后的坐标为( )
A.(3,6)
B.(1,3)
C.(1,6)
D.(6,6) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到点P处再测得点C的仰角为45°,已知OA=100米,山坡坡角为
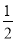 (tan∠PAB=
(tan∠PAB=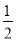 )且OAB在同一条直线上,求电视塔OC的高度以及此人所在位置的P的垂直高度。(测倾器的高度不计,结果保留根号)
)且OAB在同一条直线上,求电视塔OC的高度以及此人所在位置的P的垂直高度。(测倾器的高度不计,结果保留根号)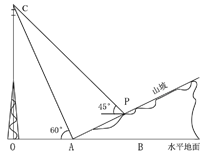
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a>b,那么3-2a>3-2b。()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE垂直平分AB,DE=2cm.求BC的长.

相关试题

