【题目】如图,Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE垂直平分AB,DE=2cm.求BC的长. 
参考答案:
【答案】解:∵DE垂直平分AB于E,
∴AD=BD,
∴∠B=∠DAB,
∵AD为∠CAB的角平分线,∠C=90°,
∴∠B=∠DAB=∠CAD,CD=DE,
∵∠B+∠CAB=90°,
∴∠B=30°,
∴BD=2DE,
∵DE=2cm,
∴CD=2cm,BD=4cm,
∴BC=6cm.
【解析】通过DE垂直平分AB于E,推出AD=BD,可得∠B=∠DAB,然后,由AD为∠CAB的角平分线,∠C=90°,根据三角形内角和定理,可知∠B=∠DAB=∠CAD=30°,同时也可推出,CD=DE,BD=2DE,由DE=2,即可推出BC的长度.
【考点精析】认真审题,首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在AC上,点E在AB上,且AB=AC,BD=BC,AD=DE=BE.求∠A的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到点P处再测得点C的仰角为45°,已知OA=100米,山坡坡角为
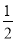 (tan∠PAB=
(tan∠PAB=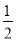 )且OAB在同一条直线上,求电视塔OC的高度以及此人所在位置的P的垂直高度。(测倾器的高度不计,结果保留根号)
)且OAB在同一条直线上,求电视塔OC的高度以及此人所在位置的P的垂直高度。(测倾器的高度不计,结果保留根号)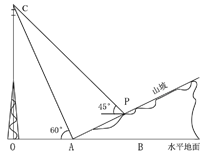
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a>b,那么3-2a>3-2b。()
-
科目: 来源: 题型:
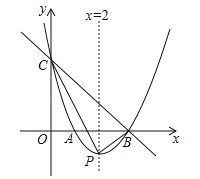
查看答案和解析>>【题目】如图,直线y=﹣x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线
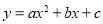 与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.(1)求该抛物线的解析式;
(2)连接PB、PC,求△PBC的面积;
(3)连接AC,在x轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(-2,-3)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<﹣2
B.k<2
C.k>2
D.k<2且k≠1
相关试题

