搜索
【题目】解方程：
（1）x2﹣4x﹣4=0；
（2）x（x﹣2）=15．
参考答案：
【答案】
（1）解：△=b2﹣4ac=（﹣4）2﹣4×1×（﹣4）=32，
=2± 
，
所以x1=2+ ，x2=2﹣ ；
（2）解：原方程可变形为x2﹣2x﹣15=0，
（x﹣5）（x+3）=0，
x﹣5=0或x+3=0，
所以x1=5，x2=﹣3．
【解析】（1）先计算判别式的值，然后利用求根公式解方程。
（2）先把方程化为一般式，然后利用因式分解法解方程．
【考点精析】根据题目的已知条件，利用公式法和因式分解法的相关知识可以得到问题的答案，需要掌握要用公式解方程，首先化成一般式．调整系数随其后，使其成为最简比．确定参数abc，计算方程判别式．判别式值与零比，有无实根便得知．有实根可套公式，没有实根要告之；已知未知先分离，因式分解是其次．调整系数等互反，和差积套恒等式．完全平方等常数，间接配方显优势．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线AB经过点A（6，0）、B（0，6），⊙O的半径为2（O为坐标原点），点P是直线AB上的一动点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（ ）
A.
B.3
C.3
D.
-
科目： 来源： 题型：
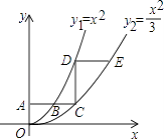
查看答案和解析>>【题目】如图，平行于x轴的直线AC分别交函数y1=x2（x≥0）与y2=
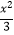（x≥0）的图象于B、C两点，过点C作y轴的平行线交y1的图象于点D，直线DE∥AC，交y2的图象于点E，则 
= ． 
-
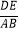科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．
（1）如果∠A=80°，求∠BPC的度数；
（2）如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q、∠A之间的数量关系．
（3）如图③，延长线段BP、QC交于点E，△BQE中，存在一个内角等于另一个内角的2倍，求∠A的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某园艺公司对一块直角三角形的花圃进行改造，测得两直角边长为6m、8m．现要将其扩建成等腰三角形，且扩充部分是以8m为直角边的直角三角形．求扩建后的等腰三角形花圃的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕矩形ABCD（AB＜BC）的对角线的交点O旋转（①→②→③），图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点．
（1）该学习小组成员意外的发现图①（三角板一直角边与OD重合）中，BN2＝CD2+CN2，在图③中（三角板一边与OC重合），CN2＝BN2+CD2，请你对这名成员在图①和图③中发现的结论选择其一说明理由．
（2）试探究图②中BN、CN、CM、DM这四条线段之间的数量关系，写出你的结论，并说明理由．
-
科目： 来源： 题型：
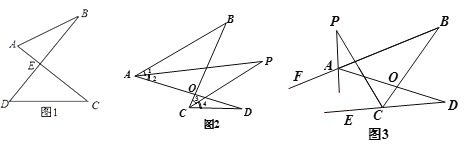
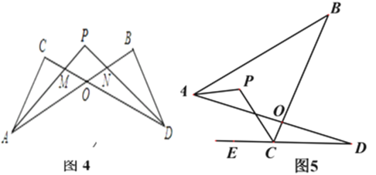
查看答案和解析>>【题目】（问题背景）
（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；
（简单应用）
（2）如图2， AP、CP分别平分∠BAD． ∠BCD，若∠ABC=46°，∠ADC=26°，求∠P的度数；
（问题探究）
（3）如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．
（拓展延伸）
（4） ①在图4中，若设∠C=α，∠B=β，∠CAP=
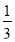∠CAB，∠CDP=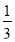∠CDB，试问∠P与∠C、∠B之间的数量关系为： （用α、β表示∠P）；②在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE， 猜想∠P与∠B、∠D的关系，直接写出结论．
相关试题
