【题目】如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.![]()
B.3
C.3 ![]()
D.![]()
参考答案:
【答案】D
【解析】连接OP、OQ.
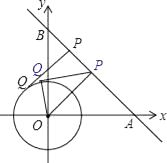
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2﹣OQ2,
∵当PO⊥AB时,线段PQ最短;
又∵A(﹣6,0)、B(0,6),
∴OA=OB=6,
∴AB=6 ![]()
∠BOP=45°,即OP是Rt△AOB斜边上的中线,
∴OP= ![]() AB=3
AB=3 ![]() ,
,
∵OQ=2,
∴PQ= ![]() ,
,
所以答案是:D.
【考点精析】本题主要考查了垂线段最短和直角三角形斜边上的中线的相关知识点,需要掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;直角三角形斜边上的中线等于斜边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1的各边长按原法延长一倍得到正方形A2B2C2D2;以此进行下去…则正方形A4B4C4D4的面积为_____;正方形AnBnCnDn的面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1, ⊙O是等边三角形
 的外接圆,
的外接圆,  是⊙O上的一个点.
是⊙O上的一个点.
(1)则 =;
=;
(2)试证明: ;
;
(3)如图2,过点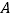 作⊙O的切线交射线
作⊙O的切线交射线  于点
于点  .
.
①试证明: ;
;
②若 ,求
,求  的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在3×3的方格中,点A、B、C、D、E、F都是格点,从A、D、E、F四点中任意取一点,以所取点及B、C为顶点画三角形,所画三角形是直角三角形的概率是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
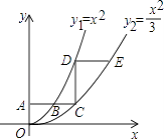
查看答案和解析>>【题目】如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2=
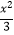 (x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则
(x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,则 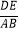 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2﹣4x﹣4=0;
(2)x(x﹣2)=15.
相关试题

