【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
(1)该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由.

(2)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
参考答案:
【答案】(1)详见解析;(2)CM2+CN2=DM2+BN2,理由详见解析.
【解析】
(1)图①连接DN,根据矩形的性质与垂直平分线的性质可得BN=DN,在Rt△CDN中,利用勾股定理即可得证;连接AN,同理也可证图③;
(2)延长MO交AB于E,连接NE、NM.通过“角边角”证明△BEO≌△DMO(ASA), 得OE=OM,BE=DM,根据垂直平分线的性质可得NE=NM,然后在Rt△BNE与Rt△CNM中,利用勾股定理与等量代换即可得CM2+CN2=DM2+BN2.
解:(1)选择图①证明:连接DN,
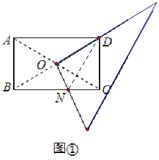
∵四边形ABCD是矩形,
∴BO=DO,∠DCN=90°,
∵ON⊥BD,
∴NB=ND,
∵∠DCN=90°,
∴ND2=NC2+CD2,
∴BN2=NC2+CD2;
(2)CM2+CN2=DM2+BN2.理由如下:
如图②,延长MO交AB于E,连接NE、NM.
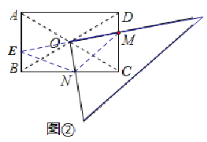
∵四边形ABCD是矩形,
∴BO=DO,∠ABC=∠DCB=90°,
∵AB∥CD,
∴∠ABO=∠CDO,∠BEO=∠DMO,
∴△BEO≌△DMO(ASA),
∴OE=OM,BE=DM,
∵NO⊥EM,
∴NE=NM,
∵∠ABC=∠DCB=90°,
∴NE2=BE2+BN2,NM2=CN2+CM2,
∴CN2+CM2=BE2+BN2,
即CN2+CM2=DM2+BN2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2﹣4x﹣4=0;
(2)x(x﹣2)=15. -
科目: 来源: 题型:
查看答案和解析>>【题目】某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题背景)
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
(简单应用)
(2)如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=46°,∠ADC=26°,求∠P的度数;
(问题探究)
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
(拓展延伸)
(4) ①在图4中,若设∠C=α,∠B=β,∠CAP=
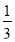 ∠CAB,∠CDP=
∠CAB,∠CDP=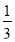 ∠CDB,试问∠P与∠C、∠B之间的数量关系为: (用α、β表示∠P);
∠CDB,试问∠P与∠C、∠B之间的数量关系为: (用α、β表示∠P);②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE, 猜想∠P与∠B、∠D的关系,直接写出结论.
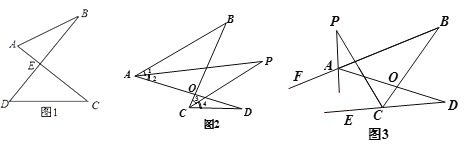
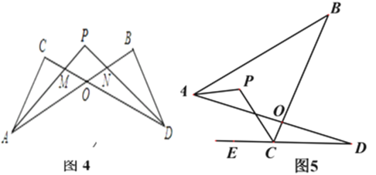
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A. 对我市市民实施低碳生活情况的调查
B. 对我国首架大型民用飞机零部件的检查
C. 对全国中学生心理健康现状的调查
D. 对市场上的冰淇淋质量的调查
相关试题

