【题目】如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90°,BC=10cm,AC=6cm,则DF=cm.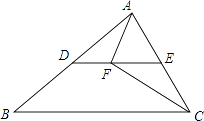
参考答案:
【答案】2
【解析】解:方法一:如图,延长AF交BC于H, 
∵点D,点E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴AF=FH,
∵∠AFC=90°,
∴CF垂直平分AH,
∴CH=AC=6cm,
∵BC=10cm,
∴BH=BC﹣CH=10﹣6=4cm,
在△ABH中,DF是中位线,
∴DF= ![]() BH=
BH= ![]() ×4=2cm;
×4=2cm;
方法二:∵点D,点E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE= ![]() BC=
BC= ![]() ×10=5cm,
×10=5cm,
∵∠AFC=90°,E是AC的中点,
∴EF= ![]() AC=
AC= ![]() ×6=3cm,
×6=3cm,
∴DF=DE﹣EF=5﹣3=2cm.
所以答案是:2.
【考点精析】掌握直角三角形斜边上的中线和三角形中位线定理是解答本题的根本,需要知道直角三角形斜边上的中线等于斜边的一半;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径是8,AB是⊙O的直径,M为AB上一动点,
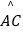 =
= 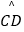 =
= 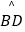 ,则CM+DM的最小值为 .
,则CM+DM的最小值为 . 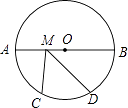
-
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空,并在括号内注明说理依据.
如图,已知
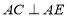 ,
,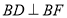 ,
,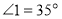 ,
,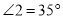 ,
,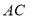 与
与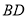 平行吗?
平行吗?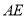 与
与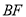 平行吗?
平行吗?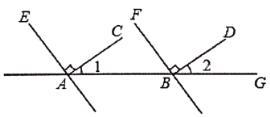
解:因为
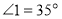 ,
,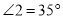 (已知),
(已知),所以
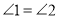 .
.所以
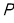 ( ).
( ).又因为
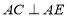 (已知),
(已知),所以
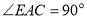 .( )
.( )所以
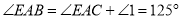 .
.同理可得,
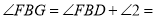
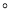 .
.所以
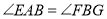 ( ).
( ).所以
 (同位角相等,两直线平行).
(同位角相等,两直线平行). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠BOE=4∶1,则∠AOF等于( )

A. 130°
B. 120°
C. 110°
D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是cm.
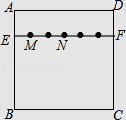
-
科目: 来源: 题型:
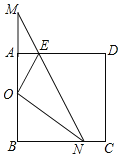
查看答案和解析>>【题目】如图,已知Rt△MBN的两条直角边与正方形ABCD的两邻边重合,∠M=30°,O为AB中点,NO平分∠BNM,EO平分∠AEN.
(1)求证:△MON为等腰三角形;
(2)求证:EN=AE+BN.
相关试题

