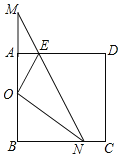
【题目】如图,已知Rt△MBN的两条直角边与正方形ABCD的两邻边重合,∠M=30°,O为AB中点,NO平分∠BNM,EO平分∠AEN.
(1)求证:△MON为等腰三角形;
(2)求证:EN=AE+BN.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1) 根据三角形内角和定理、角平分线的性质和等角对等边证得站论.
(2)延长EO交CB的延长线于点P,构造全等三角形; △AOE≌△BOP,结合全等三角形的判定与性质进行解答.
(1)证明:∵∠B=90°,∠M=30°,
∴∠BNM=60°,
∵NO平分∠BNM,
∴∠ONM=![]() ∠BNM=30°,
∠BNM=30°,
∴∠ONM=∠M,
∴OM=ON,
∴MON为等腰三角形;
(2)证明:如图,延长EO交CB延长线于点P.
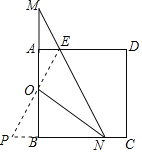
依题意得:∠BAE=∠ABP=90°.
∵O为AB中点,
∴OA=OB,
在△AOE和△BOP中,
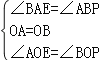 ,
,
∴△AOE≌△BOP(ASA),
∴AE=BP,OE=OP.
又NO平分∠BNM,
∴ON⊥EP,
∴EN=PN,
∴EN=PN=BP+BN=AE+BN,
∴EN=AE+BN.
-
科目: 来源: 题型:
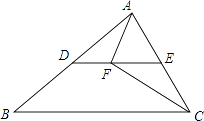
查看答案和解析>>【题目】如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90°,BC=10cm,AC=6cm,则DF=cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是cm.
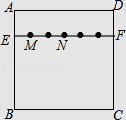
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,取两根木条a、b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.你能说出其中的一些邻补角与对顶角吗?两根木条所成的角中,如果∠α=35°,其它三个角各等于多少度?如果∠α等于90°,115°,m°呢?
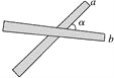
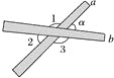
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD内接于⊙O,E是
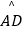 的中点,连接BE、CE,则∠ABE=°.
的中点,连接BE、CE,则∠ABE=°. 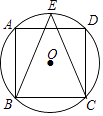
-
科目: 来源: 题型:
查看答案和解析>>【题目】用边长相等的下列两种正多边形,不能进行平面镶嵌的是( )
A. 等边三角形和正六边形 B. 正方形和正八边形
C. 正五边形和正十边形 D. 正六边形和正十二边形
相关试题

