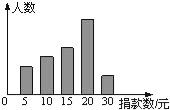
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.
(1)他们一共抽查了多少人捐款数不少于20元的概率是多少?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有2310名学生,请估算全校学生共捐款多少元?
参考答案:
【答案】(1)![]() ;(2)众数是20元,中位数是15元;(3)全校学生共捐款36750元.
;(2)众数是20元,中位数是15元;(3)全校学生共捐款36750元.
【解析】
试题(1)由条形图可得抽查的总人数;
(2)众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;
(3)求出这组数据的平均数,再估算.
(1)设捐15元的人数为5x,则根据题意捐20元的人数为8x.
∴5x+8x=39,∴x=3,
∴一共调查了3x+4x+5x+8x+2x=66(人),
∴捐款数不少于20元的概率是![]() .
.
(2)由(1)可知,这组数据的众数是20(元),中位数是15(元).
(3)全校学生共捐款:
(9×5+12×10+15×15+24×20+6×30)÷66×2310=36750(元).
-
科目: 来源: 题型:
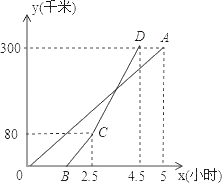
查看答案和解析>>【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.
(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把一根绳子对折后得到的图形为线段AB,从点P处把绳子剪断,已知AP:BP=4:5,若剪断后的各段绳子中最长的一段为80cm,则绳子的原长为________ cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水,每户每月水费按如下标准收费:月用水量不超过8立方米,按每立方米a元收取;月用水量超过8立方米但不超过14立方米的部分,按每立方米b元收取;月用水量超过14立方米的部分,按每立方米c元收取.下表是某月部分居民的用水量及缴纳水费的数据.
用水量(立方米)
2.5
15
6
12
10.3
4.7
9
17
16
水费(元)
5
33.4
12
25.6
21.52
9.4
18.4
39.4
36.4
(1) ①a= _____,b= _____,c= _____;
②若小明家七月份需缴水费31元,则小明家七月份用水 米3;
(2) 该市某用户两个月共用水30立方米,设该用户在其中一个月用水x立方米,请列式表示这两个月该用户应缴纳的水费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x<3时,y1<y2中.则正确的序号有________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2,x3,…x2016都是不等于0的有理数,若y1=
 ,求y1的值.
,求y1的值.当x1>0时,y1=
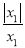 =
= =1;当x1<0时,y1=
=1;当x1<0时,y1= =
= =﹣1,所以y1=±1
=﹣1,所以y1=±1(1)若y2=
 +
+ ,求y2的值
,求y2的值(2)若y3=
 +
+ +
+ ,则y3的值为 ;
,则y3的值为 ;(3)由以上探究猜想,y2016=
 +
+ +
+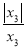 +…+
+…+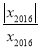 共有 个不同的值,在y2016这些不同的值中,最大的值和最小的值的差等于 .
共有 个不同的值,在y2016这些不同的值中,最大的值和最小的值的差等于 .
相关试题

