【题目】如图,AB为⊙O的直径,D为 ![]() 的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E. 
(1)求证:DE是⊙O的切线;
(2)连接CD,若OA=AE=4,求四边形ACDE的面积.
参考答案:
【答案】
(1)证明:∵D为 ![]() 的中点,
的中点,
∴OD⊥AC,
∵AC∥DE,
∴OD⊥DE,
∴DE是⊙O的切线
(2)解:连接DC,

∵D为 ![]() 的中点,
的中点,
∴OD⊥AC,AF=CF,
∵AC∥DE,且OA=AE,
∴F为OD的中点,即OF=FD,
在△AFO和△CFD中,

∴△AFO≌△CFD(SAS),
∴S△AFO=S△CFD,
∴S四边形ACDE=S△ODE
在Rt△ODE中,OD=OA=AE=4,
∴OE=8,
∴DE= ![]() =4
=4 ![]() ,
,
∴S四边形ACDE=S△ODE= ![]() ×OD×DE=
×OD×DE= ![]() ×4×4
×4×4 ![]() =8
=8 ![]() .
.
【解析】(1)欲证明DE是⊙O的切线,只要证明AC⊥OD,ED⊥OD即可.(2)由△AFO≌△CFD(SAS),推出S△AFO=S△CFD , 推出S四边形ACDE=S△ODE , 求出△ODE的面积即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=_______,△APE的面积等于8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=4.8cm,点C是线段AB的中点,点D是线段CB的中点,点E在线段AB上,且CE=
 AC,画图并计算DE的长.
AC,画图并计算DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程
已知a、b、c为△ABC为三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4①
∴c2(a2-b2)=(a2-b2)(a2+b2)②
∴c2=a2+b2③
∴△ABC是直角三角形
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的序号________.
(2)错误原因为________.
(3)本题正确结论是什么,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知数轴上点A、B分别表示a、b,且|b+6|与(a﹣9)2互为相反数,O为原点.
(1)a= ,b= ;
(2)若将数轴折叠点A与表示﹣10的点重合,则与点B重合的点所表示的数为 ;
(3)若点M、N分别从点A、B同时出发,点M以每秒1个单位长度的速度沿数轴向左匀速运动,点N以每秒2个单位长度的速度沿数轴向右匀速运动,N到点A后立刻原速返回,设运动时间为t(t>0)秒.①点M表示的数是 (用含t的代数式表示);②求t为何值时,2MO=MA;③求t为何值时,点M与N相距3个单位长度.
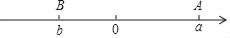
-
科目: 来源: 题型:
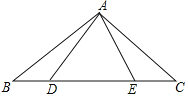
查看答案和解析>>【题目】如图,点D,E在△ABC的边BC上,连接AD,AE.有下面三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成三个命题.解答下列问题
(1)写出这三个命题,并直接判断其是否是真命题;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
相关试题

