【题目】在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 的纵坐标满足
的纵坐标满足![]() , 则称点
, 则称点![]() 是点
是点![]() 的“绝对点”.
的“绝对点”.
(![]() )点
)点![]() 的“绝对点”的坐标为.
的“绝对点”的坐标为.
(![]() )点
)点![]() 是函数
是函数![]() 的图像上的一点,点
的图像上的一点,点![]() 是点
是点![]() 的“绝对点”.若点
的“绝对点”.若点![]() 与点
与点![]() 重合,求点
重合,求点![]() 的坐标.
的坐标.
(![]() )点
)点![]() 的“绝对点”
的“绝对点”![]() 是函数
是函数![]() 的图像上的一点.当
的图像上的一点.当![]() 时,求线段
时,求线段![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() ;(2)点P的坐标为
;(2)点P的坐标为![]() ;(3)
;(3)![]() 的最大值为14或2.
的最大值为14或2.
【解析】试题分析:(1)根据绝对的定义,可得答案;(2)根据绝对的定义,可得P点的坐标,根据点在函数图象上,可得方程,根据解方程,可得答案;(3)根据关联点的定义,可得![]() 的坐标,根据平行于y的直线上两点间的距离,可得二次函数,根据二次函数的性质,可得答案
的坐标,根据平行于y的直线上两点间的距离,可得二次函数,根据二次函数的性质,可得答案
试题解析:( ![]() )
)![]() .
.
(![]() )设点
)设点![]() 的坐标为
的坐标为![]() ,
,
当![]() 时,
时, ![]() 的坐标为
的坐标为![]() ,
,
若![]() 与
与![]() 重合,则
重合,则![]() ,
,
又![]() ,
,
所以![]() .
.
即![]() 的坐标为
的坐标为![]() 或
或![]() ,
,
又![]() 不符合题意,舍去,
不符合题意,舍去,
所以![]() 的坐标为
的坐标为![]() .
.
当![]() 时,
时, ![]() 的坐标为
的坐标为![]() .可得
.可得![]() ,舍去.
,舍去.
综上所述,点![]() 的坐标为
的坐标为![]() .
.
(![]() )当
)当![]() 时,
时, ![]() 的坐标为
的坐标为![]() ,
,
因为![]() 是函数
是函数![]() 的图像上一点,
的图像上一点,
所以![]() ,
,
即![]() .
.
![]() .
.
由图像可知,当![]() 时,
时, ![]() 的最大值为
的最大值为![]() .
.
当![]() 时,
时, ![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() 的最大值为
的最大值为![]() .
.
综上所述, ![]() 的最大值为
的最大值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
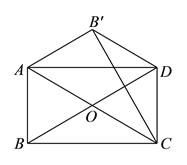
查看答案和解析>>【题目】如图,在矩形
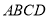 中,对角线
中,对角线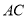 、
、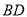 交于点
交于点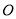 ,将
,将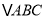 沿直线
沿直线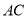 翻折,点
翻折,点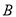 落在点
落在点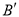 处,且
处,且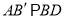 ,连接
,连接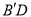 .求证:
.求证:(
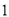 )
)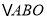 是等边三角形.
是等边三角形.(
 )
)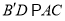 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
旋转是图形的一种变换方式,利用旋转来解决几何问题往往可以使解题过程更简单,起到事半功倍的效果.
初步思考
(
 )如图①,点
)如图①,点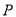 是等边
是等边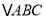 内部一点,且
内部一点,且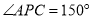 ,
, 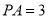 ,
, 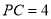 .求
.求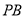 的长.
的长.小敏在解答此题时,利用了“旋转法”进行证明,她的方法如下:
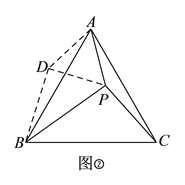
如图②,将
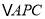 绕点
绕点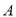 按顺时针方向旋转
按顺时针方向旋转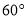 后得到
后得到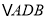 ,连接
,连接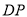 .(请你在下面的空白处完成小敏的证明过程.)
.(请你在下面的空白处完成小敏的证明过程.)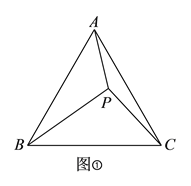
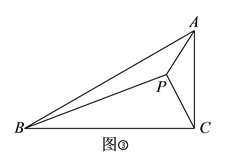
推广运用
(
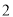 )如图③,在
)如图③,在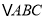 中,
中, 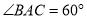 ,
, 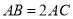 ,点
,点 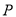 是
是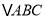 内部一点,且
内部一点,且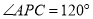 ,
, 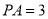 ,
,  .求
.求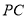 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A. 两直线平行,则同位角相等B. 同旁内角互补,则两直线平行
C. 三角形内角和为180°D. 三角形一个外角大于任何一个内角
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算6x3.(-2x2y)=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a2﹣4ab+5b2﹣2b+1=0,则以a,b为根的一元二次方程为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个正三角形,分别连接这个正三角形各边上的中点得到图2,再连接图2中间的小三角形各边上的中点得到图3,按此方法继续下去.前三个图形中三角形的个数分别是1个,5个,9个,那么第5个图形中三角形的个数是个;第n个图形中三角形的个数是个.

相关试题

