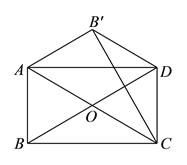
【题目】如图,在矩形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,且
处,且![]() ,连接
,连接![]() .求证:
.求证:
(![]() )
)![]() 是等边三角形.
是等边三角形.
(![]() )
)![]() .
.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由四边形ABCD是矩形,得到∠BAD=90°,AO=OD,得到∠OAD=∠ADO,根据平行线的性质得到∠B′AD=∠ADB,等量代换得到∠B′AD=∠DAC,根据折叠的性质得到∠BAC=∠CAB′,得到∠DAC=![]() ∠BAC,求得∠BAC=60°,于是得到结论;(2)连接B′O,推出B′C垂直平分OD,得到B′O=B′D,根据等腰三角形的性质得到∠OB′C=∠OCB′=30°,求得∠OCB′=∠CB′D,于是得到结论.
∠BAC,求得∠BAC=60°,于是得到结论;(2)连接B′O,推出B′C垂直平分OD,得到B′O=B′D,根据等腰三角形的性质得到∠OB′C=∠OCB′=30°,求得∠OCB′=∠CB′D,于是得到结论.
试题解析:( ![]() )∵四边形
)∵四边形![]() 是矩形,
是矩形,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 是由
是由![]() 沿直线
沿直线![]() 翻折得到,
翻折得到,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() 是等边三角形.
是等边三角形.
(![]() )∵
)∵![]() 是由
是由![]() 沿直线
沿直线![]() 翻折得到,
翻折得到,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=2(x+1)2﹣3的顶点坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(m﹣1,2m+1)在第一象限,则m的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】10个人围成一圈做游戏.游戏的规则是:每个人心里都想一个数,并把目己想的数告许与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报出来的数是3的人心里想的数是( )
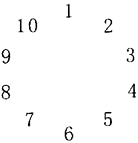
A. 2
B.﹣2
C.4
D.﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
旋转是图形的一种变换方式,利用旋转来解决几何问题往往可以使解题过程更简单,起到事半功倍的效果.
初步思考
(
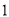 )如图①,点
)如图①,点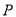 是等边
是等边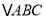 内部一点,且
内部一点,且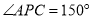 ,
, 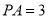 ,
, 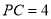 .求
.求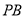 的长.
的长.小敏在解答此题时,利用了“旋转法”进行证明,她的方法如下:
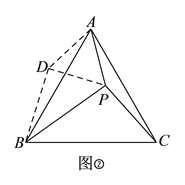
如图②,将
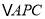 绕点
绕点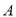 按顺时针方向旋转
按顺时针方向旋转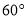 后得到
后得到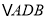 ,连接
,连接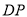 .(请你在下面的空白处完成小敏的证明过程.)
.(请你在下面的空白处完成小敏的证明过程.)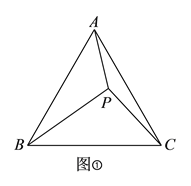
推广运用
(
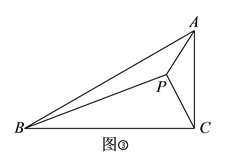
 )如图③,在
)如图③,在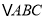 中,
中, 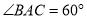 ,
, 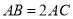 ,点
,点 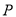 是
是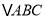 内部一点,且
内部一点,且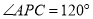 ,
, 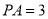 ,
,  .求
.求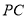 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A. 两直线平行,则同位角相等B. 同旁内角互补,则两直线平行
C. 三角形内角和为180°D. 三角形一个外角大于任何一个内角
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
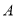 的坐标为
的坐标为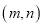 ,若点
,若点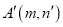 的纵坐标满足
的纵坐标满足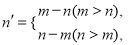 , 则称点
, 则称点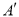 是点
是点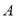 的“绝对点”.
的“绝对点”.(
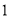 )点
)点 的“绝对点”的坐标为.
的“绝对点”的坐标为.(
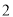 )点
)点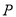 是函数
是函数 的图像上的一点,点
的图像上的一点,点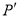 是点
是点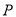 的“绝对点”.若点
的“绝对点”.若点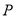 与点
与点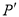 重合,求点
重合,求点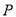 的坐标.
的坐标.(
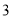 )点
)点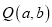 的“绝对点”
的“绝对点”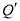 是函数
是函数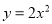 的图像上的一点.当
的图像上的一点.当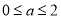 时,求线段
时,求线段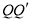 的最大值.
的最大值.
相关试题

