Question

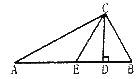
【题目】如图，CD是△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处．

(1)求∠A的度数；

(2)若，求△AEC的面积．

Answer 1

【答案】 (1)∠A的度数为30°; (2) △AEC面积为.

【解析】分析：(1)根据直角三角形斜边上的中线等于斜边的一半可得到AC=AE，从而得到∠A=∠ACE，再由折叠的性质及三角形的外角性质得到∠B=2∠A，从而不难求得∠A的度数．(2)由(1)得∠A=30°，据解直角三角形得△CEB是等边三角形，继而求解.

本题解析：(1)∵E是AB中点，∴CE为Rt△ACB斜边AB上的中线。AE=BE=CE=AB，。

∵CE=CB．∴△CEB为等边三角形。

∴ ∠CEB=60°。 ∵ CE=AE．∴∠A=∠ACE=30°。

故∠A的度数为30°。

(2)∵Rt△ACB中，∠A=30°，∴tanA ,

∴ AC= ，BC=1,∴△CEB是等边三角形，CD⊥BE，∴CD=,

∵AB=2BC=2,∴ ,∴S△ACE=,

即△AEC面积为 。