【题目】综合题
(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,试探索∠1+∠2与∠A的关系.(不必证明). 
(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,求∠BIC的度数; 
(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论. 
参考答案:
【答案】
(1)解:∠1+∠2=2∠A
(2)解:由(1)∠1+∠2=2∠A,得2∠A=130°,∴∠A=65°
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB= ![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
= ![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣ ![]() ∠A,
∠A,
∴∠BIC=180°﹣(∠IBC+∠ICB),
=180°﹣(90°﹣ ![]() ∠A)=90°+
∠A)=90°+ ![]() ×65°=122.5°
×65°=122.5°
(3)解:∵BF⊥AC,CG⊥AB,∴∠AFH+∠AGH=90°+90°=180°,
∠FHG+∠A=180°,∴∠BHC=∠FHG=180°﹣∠A,由(1)知∠1+∠2=2∠A,
∴∠A= ![]() (∠1+∠2),
(∠1+∠2),
∴∠BHC=180°﹣ ![]() (∠1+∠2)
(∠1+∠2)
【解析】(1)根据翻折变换的性质以及三角形内角和定理以及平角的定义求出即可;(2)根据三角形角平分线的性质得出∠IBC+∠ICB=90°﹣ ![]() ∠A,得出∠BIC的度数即可;(3)根据翻折变换的性质以及垂线的性质得出,∠AFH+∠AGH=90°+90°=180°,进而求出∠A=
∠A,得出∠BIC的度数即可;(3)根据翻折变换的性质以及垂线的性质得出,∠AFH+∠AGH=90°+90°=180°,进而求出∠A= ![]() (∠1+∠2),即可得出答案.
(∠1+∠2),即可得出答案.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=﹣1是一元二次方程x2+mx+3=0的一个解,则m的值是( )
A.4B.﹣4C.﹣3D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径FD⊥弦AB于点H,E是
 上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.
上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.
(1)求⊙O的直径FD;
(2)在E点运动的过程中,EFCF的值是否为定值?若是,求出其定值;若不是,请说明理由;
(3)当E点运动到
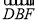 的中点时,连接AE交DF于点G,求△FEA的面积.
的中点时,连接AE交DF于点G,求△FEA的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形ECGF的边长分别为a和6,
(1) 写出表示阴影部分面积的代数式(结果要求化简);
(2) 求
 时,阴影部分的面积.
时,阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处.

(1)求∠A的度数;
(2)若
 ,求△AEC的面积.
,求△AEC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2014年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2016年底三年共累计投资9.5亿元人民币建设廉租房.若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2016年底共建设了多少万平方米的廉租房?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中有稳定性的是( )
A.正方形
B.长方形
C.直角三角形
D.平行四边形
相关试题

