【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.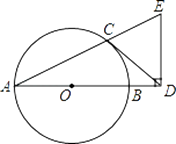
(1)求证:DC=DE;
(2)若tan∠CAB= ![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
参考答案:
【答案】
(1)
证明:连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ACO+∠DCE=90°,
又∵ED⊥AD,∴∠EDA=90°,
∴∠EAD+∠E=90°,
∵OC=OA,∴∠ACO=∠EAD,
故∠DCE=∠E,
∴DC=DE,
(2)
解:设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,
在Rt△EAD中,
∵tan∠CAB= ![]() ,∴ED=
,∴ED= ![]() AD=
AD= ![]() (3+x),
(3+x),
由(1)知,DC= ![]() (3+x),在Rt△OCD中,
(3+x),在Rt△OCD中,
OC2+CD2=DO2,
则1.52+[ ![]() (3+x)]2=(1.5+x)2,
(3+x)]2=(1.5+x)2,
解得:x1=﹣3(舍去),x2=1,
故BD=1.
【解析】(1)根据“等角对等边”,从证∠DCE=∠E出发,连接OC,根据两个直角,去找相关角的数量关系;
(2)根据勾股定理构造方程去解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组勾股数:
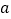
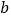
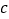
第1组
3=2×1+1
4=2×1×(1+1)
5=2×1×(1+1)+1
第2组
5=2×2+1
12=2×2×(2+1)
13=2×2×(2+1)+1
第3组
7=2×3+1
24=2×3×(3+1)
25=2×3×(3+1)+1
第4组
9=2×4+1
40=2×4×(4+1)
41=2×4×(4+1)+1
…
…
…
…
观察以上各组勾股数的特点:
(1)请写出第7组勾股数
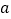 ,
,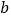 ,
,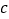 ;
;(2)写出第
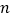 组勾股数
组勾股数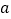 ,
,,
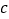 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由. -
科目: 来源: 题型:
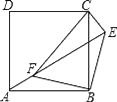
查看答案和解析>>【题目】如图所示,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为
(2)求点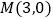 到直线
到直线 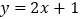 的距离;
的距离;
(3)如果点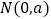 到直线
到直线 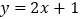 的距离为3,求a的值.
的距离为3,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

相关试题

