【题目】设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为
(2)求点 ![]() 到直线
到直线 ![]() 的距离;
的距离;
(3)如果点 ![]() 到直线
到直线 ![]() 的距离为3,求a的值.
的距离为3,求a的值.
参考答案:
【答案】
(1)4
(2)
解:直线 ![]() 记为
记为 ![]() ,过点
,过点 ![]() 作
作 ![]() ,垂足为点
,垂足为点 ![]() ,
,
设 ![]() 与
与 ![]() 轴的交点分别为
轴的交点分别为 ![]() ,则
,则 ![]() .
.
∴ ![]() .
.
∵ ![]()
∴ ![]() ,即
,即 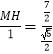 .∴
.∴ ![]() .
.
∴点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() .
.
(3)
![]()
【解析】(1)OP=![]() =5,
=5,
点O(0,0)到⊙P的距离为5-1=4;
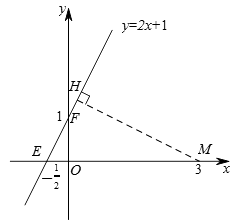
(2)直线 y = 2 x + 1 记为 l ,过点 M 作 M H ⊥ l ,垂足为点 H ,
设 ![]() 与
与 ![]() 轴的交点分别为
轴的交点分别为 ![]() ,则
,则 ![]() .
.
图1
∴ ![]() .
.
∵ ![]()
∴ ![]() ,即
,即 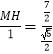 .∴
.∴ ![]() .
.
∴点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() .
.
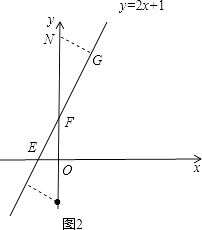
(3)②N在F点的上边,如图2,过点N作NG⊥l,垂足为点G,
∵△EOF∽△NGF,
∴![]() =
=![]() ,
,
即![]()
![]() ,
,
∴a=1+3![]() ;
;
N在F点的下边,
同理可得a=1-3![]() ;
;
故a=1±3![]() .
. 
(1)根据勾股定理可得点O(0,0)到⊙P的距离;
(2)过点M作MH⊥l,垂足为点H,通过证明△EOF∽△MHE,由相似三角形的性质可得MH , 从而得到点M到直线y=2x+1的距离;
(3)分两种情况:N在F点的上边;N在F点的下边;进行讨论先得到EN的长,进一步即可得到a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
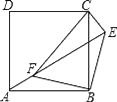
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积.
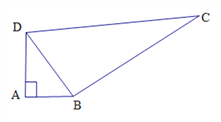
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
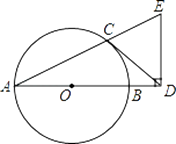
(1)求证:DC=DE;
(2)若tan∠CAB= ,AB=3,求BD的长.
,AB=3,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上A点表示数
 ,B点表示数
,B点表示数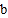 ,
,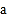 、
、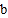 满足|
满足|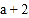 |+|
|+|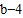 |=0;
|=0;
(1)点A表示的数为_____;点B表示的数为_____;
(2)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①当t=1时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
当t=3时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.
相关试题

