【题目】直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=0.5,OB=4,OE=2. 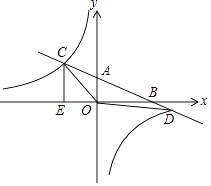
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
参考答案:
【答案】
(1)解:在Rt△AOB中,∵tan∠ABO=0.5,OB=4,
∴OA=2,
∴A(0,2),B(4,0),设直线AB的解析式为y=kx+b,则有 ![]() ,解得
,解得 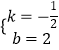 ,
,
∴直线AB的解析式为y=﹣ ![]() x+2,
x+2,
∵OE=2,CE⊥x轴,
∴C(﹣2,3),设反比例函数的解析式为y= ![]() ,
,
∴k=﹣6,
∴直线AB和反比例函数的解析式分别为y=﹣ ![]() x+2,y=﹣
x+2,y=﹣ ![]() .
.
(2)解:由 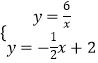 解得
解得 ![]() 或
或 ![]() ,
,
∴D(6,﹣1),
∴S△COD=S△AOC+S△AOD= ![]() ×2×2+
×2×2+ ![]() ×2×6=8.
×2×6=8.
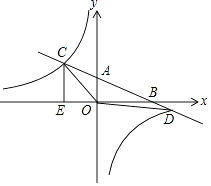
【解析】(1)在Rt△AOB中,由tan∠ABO=0.5,OB=4,推出OA=2,推出A(0,2),B(4,0),设直线AB的解析式为y=kx+b,利用待定系数法即可解决问题.(2)利用方程组求出点D坐标,根据S△COD=S△AOC+S△AOD计算即可.
【考点精析】关于本题考查的解直角三角形,需要了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,AD是
中,AD是 的平分线,
的平分线, ,垂足为E,作
,垂足为E,作 ,交直线AE于点
,交直线AE于点 设
设 ,
, .
.
 若
若 ,
, ,依题意补全图1,并直接写出
,依题意补全图1,并直接写出 的度数;
的度数; 如图2,若
如图2,若 是钝角,求
是钝角,求 的度数
的度数 用含
用含 ,
, 的式子表示
的式子表示 ;
; 如图3,若
如图3,若 ,直接写出
,直接写出 的度数
的度数 用含
用含 ,
, 的式子表示
的式子表示 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数y=
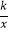 (x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 .
(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 . 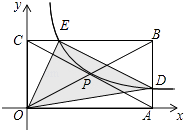
-
科目: 来源: 题型:
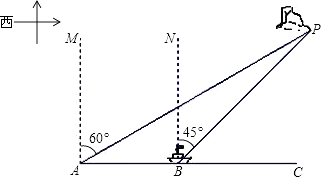
查看答案和解析>>【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点
 ,若点Q的坐标为
,若点Q的坐标为 ,其中a为常数,则称点Q是点P的“a级关联点”
,其中a为常数,则称点Q是点P的“a级关联点” 例如,点
例如,点 的“3级关联点”为
的“3级关联点”为 ,即
,即 .
. 已知点
已知点 的“
的“ 级关联点”是点
级关联点”是点 ,点B的“2级关联点”是
,点B的“2级关联点”是 ,求点
,求点 和点B的坐标;
和点B的坐标; 已知点
已知点 的“
的“ 级关联点”
级关联点” 位于y轴上,求
位于y轴上,求 的坐标;
的坐标; 已知点
已知点 ,
, ,点
,点 和它的“n级关联点”
和它的“n级关联点” 都位于线段CD上,请直接写出n的取值范围.
都位于线段CD上,请直接写出n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是( )

A. ①③④ B. ②③④ C. ①②③ D. ①②④
-
科目: 来源: 题型:
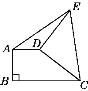
查看答案和解析>>【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为____________.
相关试题

