搜索
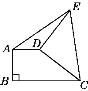
【题目】如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD＝2，将腰CD以D为中心逆时针旋转90°至DE，连接AE、CE，△ADE的面积为3，则BC的长为____________．
参考答案：
【答案】5
【解析】
过D点作DF⊥BC，垂足为F，过E点作EG⊥AD，交AD的延长线与G点，由旋转的性质可知△CDF≌△EDG，从而有CF=EG，由△ADE的面积可求EG，得出CF的长，由矩形的性质得BF=AD，根据BC=BF+CF求解．
解：过D点作DF⊥BC，垂足为F，过E点作EG⊥AD，交AD的延长线与G点，
由旋转的性质可知CD=ED，
∵∠EDG+∠CDG=∠CDG+∠FDC=90°，
∴∠EDG=∠FDC，又∠DFC=∠G=90°，
∴△CDF≌△EDG，∴CF=EG，
∵S△ADE=
AD×EG=3，AD=2，
∴EG=3，则CF=EG=3，
依题意得四边形ABFD为矩形，∴BF=AD=2，
∴BC=BF+CF=2+3=5．
故答案为：5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线AB分别与x轴、y轴交于B和A，与反比例函数的图象交于C、D，CE⊥x轴于点E，tan∠ABO=0.5，OB=4，OE=2．
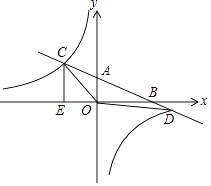
（1）求直线AB和反比例函数的解析式；
（2）求△OCD的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，对于点
，若点Q的坐标为
，其中a为常数，则称点Q是点P的“a级关联点”
例如，点
的“3级关联点”为
，即
．
已知点
的“
级关联点”是点
，点B的“2级关联点”是
，求点和点B的坐标；
已知点
的“
级关联点”
位于y轴上，求的坐标；
已知点
，
，点
和它的“n级关联点”
都位于线段CD上，请直接写出n的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△AEB和Rt△AFC中，BE与AC相交于点M，与CF相交于点D，AB与CF相交于N，∠E＝∠F＝90°，∠EAC＝∠FAB，AE＝AF.给出下列结论：①∠B＝∠C；②CD＝DN；③BE＝CF；④△ACN≌△ABM.其中正确的结论是( )
A. ①③④ B. ②③④ C. ①②③ D. ①②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．
（1）求抛物线的解析式；
（2）求△MCB的面积S△MCB ． -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
（2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在梯形ABCD中，已知AD∥BC，AB=CD，延长线段CB到E，使BE=AD，连接AE、AC.
【1】求证：△ABE≌△CDA；
【2】若∠DAC=40°，求∠EAC的度数.
相关试题
