【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 . 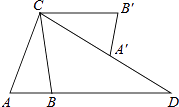
参考答案:
【答案】6
【解析】解:∵将△ABC绕点C按逆时针方向旋转得到△A′B′C,
∴AC=CA′=4,AB=B′A′=2,∠A=∠CA′B′,
∵CB′∥AB,
∴∠B′CA′=∠D,
∴△CAD∽△B′A′C,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得AD=8,
∴BD=AD﹣AB=8﹣2=6.
故答案为:6.
依据图形可知∠CAB=∠CAD,然后依据平行线的性质以及旋转的性质得出∠B′CA′=∠D,故此可证明△CAD∽△B′A′C,然后依据相似三角形的性质可求得AD的长,最后,再依据BD=AD﹣AB求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=48°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;……;∠An-1BC与∠An-1CD的平分线交于点An,要使∠An的度数为整数,则n的最大值为( )
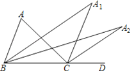
A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地有两条公路,一条是全长450公里的普通公路,一条是全长330公里的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快35公里/小时,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半.如果设该客车由高速公路从甲地到乙地所需时间为x小时,那么x满足的分式方程是( )
A.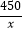 =
= 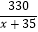 ×2
×2
B.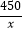 =
= 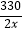 ﹣35
﹣35
C.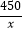 ﹣
﹣ 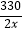 =35
=35
D.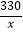 ﹣
﹣  =35
=35 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( )
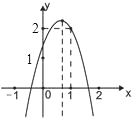
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某段铁路两旁安置了两座可旋转探照灯,主道路是平行,即PQ∥MN. 如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度. 若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动_________秒,两灯的光束互相平行.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C';
(2)在BC上找一点P,使AP平分△ABC的面积;
(3)试在直线l上画出所有的格点Q,使得由点A'、B'、C'、Q四点围成的四边形的面积为9.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
相关试题

