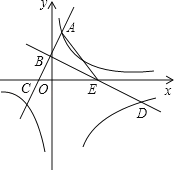
【题目】如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=![]() 的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y=
的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y=![]() (x>0)的图象交于点D(n,﹣2).
(x>0)的图象交于点D(n,﹣2).
(1)k1和k2的值分别是多少?
(2)直线AB,BD分别交x轴于点C,E,若F是y轴上一点,且满足△BDF∽△ACE,求点F的坐标.
参考答案:
【答案】(1)4,-16;(2)点F的坐标为(0,﹣8).
【解析】(1)将A坐标代入一次函数解析式中求出m的值,确定出A的坐标,将A坐标代入反比例函数y=![]() 中即可求出k1的值;过A作AM垂直于y轴,过D作DN垂直于y轴,可得出一对直角相等,再由AC垂直于BD,利用同角的余角相等得到一对角相等,利用两对对应角相等的两三角形相似得到△ABM与△BDN相似,由相似得比例,求出DN的长,确定出D的坐标,代入反比例函数y=
中即可求出k1的值;过A作AM垂直于y轴,过D作DN垂直于y轴,可得出一对直角相等,再由AC垂直于BD,利用同角的余角相等得到一对角相等,利用两对对应角相等的两三角形相似得到△ABM与△BDN相似,由相似得比例,求出DN的长,确定出D的坐标,代入反比例函数y=![]() 中即可求出k2的值;
中即可求出k2的值;
(2)在y轴上存在一个点F,使得△BDF∽△ACE,此时F(0,-8),理由为:由y=2x+2求出C坐标,由OB=ON=2,DN=8,可得出OE为△BDN的中位线,求出OE的长,进而利用勾股定理求出AE,CE,AC,BD的长,以及∠EBO=∠ACE=∠EAC,若△BDF∽△ACE,得到比例式,求出BF的长,即可确定出此时F的坐标。
(1)∵点A(1,m)在一次函数y=2x+2的图象上,∴m=2+2=4,
∵点A(1,4)在反比例函数y=![]() 的图象上,∴k1=1×4=4;
的图象上,∴k1=1×4=4;
∵BD⊥AB,∴∠BCE+∠BEC=90°,∵∠OCB+∠OBC=90°,∴∠BEC=∠OBC,
∴△BEC∽△OBC,∴![]() .
.
∵已知一次函数y=2x+2的图象与y轴交于点B,与x轴交于点C,
∴B(0,2),C(﹣1,0),∴BC=![]() =
=![]() ,OB=2,OC=1,∴CE=
,OB=2,OC=1,∴CE=![]() =5,
=5,
∴E(4,0).设直线BD的解析式为y=kx+b,则有![]() ,解得:
,解得:![]() ,
,
∴直线BD的解析式为y=﹣![]() x+2.∵点D(n,﹣2)在直线BD上,
x+2.∵点D(n,﹣2)在直线BD上,
∴﹣2=﹣![]() n+2,解得:n=8,∵点D(8,﹣2)在反比例函数y=
n+2,解得:n=8,∵点D(8,﹣2)在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k2=8×(﹣2)=﹣16.
(2)∵A(1,4),C(﹣1,0),E(4,0),∴CE=4﹣(﹣1)=5,AE=![]() =5,
=5,
AC=![]() =2
=2![]() ,∴∠EAC=∠ECA.
,∴∠EAC=∠ECA.
∵∠EBO+∠CBO=90°,∠CBO+∠BCO=90°,∴∠EBO=∠BCO=∠EAC=∠DBF,
∴点F在点B的下方.设点F(0,t),B(0,2),D(8,﹣2),
∴BF=2﹣t,BD=![]() =4
=4![]() .∵△BDF∽△ACE,∴
.∵△BDF∽△ACE,∴![]() ,
,
∴BF=2﹣t=![]() =10,解得:t=﹣8.
=10,解得:t=﹣8.
∴当F是y轴上一点,且满足△BDF∽△ACE时,点F的坐标为(0,﹣8).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 是反比例函数
是反比例函数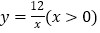 的图像上的一个动点,经过点
的图像上的一个动点,经过点 的直线
的直线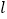 交
交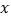 轴负半轴于点
轴负半轴于点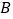 ,交
,交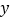 轴正半轴于点
轴正半轴于点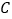 .过点
.过点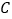 作
作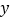 轴的垂线,交反比例函数的图像于点
轴的垂线,交反比例函数的图像于点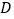 .过点
.过点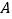 作
作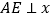 轴于点
轴于点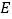 ,交
,交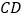 于点
于点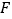 ,连接
,连接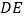 .设点
.设点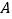 的横坐标是
的横坐标是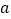 .
.(1)若
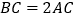 ,求点
,求点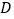 的坐标(用含
的坐标(用含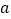 的代数式表示);
的代数式表示);(2)若
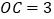 ,当四边形
,当四边形 是平行四边形时,求
是平行四边形时,求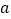 的值,并求出此时直线
的值,并求出此时直线 对应的函数表达式.
对应的函数表达式.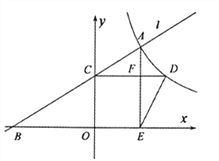
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
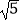 cm,且tan∠EFC=
cm,且tan∠EFC=  ,则矩形ABCD的周长是 .
,则矩形ABCD的周长是 . 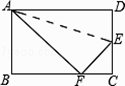
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,点
,点 从点
从点 出发,沿
出发,沿 向点
向点 匀速运动,速度为每秒1个单位,过点
匀速运动,速度为每秒1个单位,过点 作
作 ,交对角线
,交对角线 于点
于点 .点
.点 从点
从点 出发,沿对角线
出发,沿对角线 向点
向点 匀速运动,速度为每秒1个单位.
匀速运动,速度为每秒1个单位.  、
、 两点同时出发,设它们的运动时间为
两点同时出发,设它们的运动时间为 秒(
秒( ).
).(1)当
 时,求出
时,求出 的值;
的值;(2)连接
 ,当
,当 时,求出
时,求出 的值;
的值;(3)试探究:当
 为何值时,
为何值时,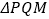 是等腰三角形?
是等腰三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△OPQ是边长为
 的等边三角形,若反比例函数y=
的等边三角形,若反比例函数y= 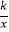 的图像过点P. (Ⅰ)求点P的坐标和k的值;
的图像过点P. (Ⅰ)求点P的坐标和k的值;
(Ⅱ)若在这个反比例函数的图像上有两个点(x1 , y1)(x2 , y2),且x1<x2<0,请比较y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学完一元一次方程解法,数学老师出了一道解方程题目:
 .李铭同学的解题步骤如下:
.李铭同学的解题步骤如下:解:去分母,得3(x+1)-2(2-3x)=1;……①
去括号,得3x+3-4-6x=1; ……②
移项,得3x-6x=1-3+4; ……③
合并同类项,得-3x=2; ……④
系数化为1,得x=-
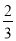 . ……⑤
. ……⑤(1)聪明的你知道李铭的解答过程在第_________(填序号)出现了错误,出现上面错误的原因是违背了____.(填序号)①去括号法则;②等式的性质1;③等式的性质2;④加法交换律.
(2)请你写出正确的解答过程.
-
科目: 来源: 题型:
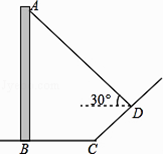
查看答案和解析>>【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
相关试题

