【题目】如图△OPQ是边长为 ![]() 的等边三角形,若反比例函数y=
的等边三角形,若反比例函数y= ![]() 的图像过点P. (Ⅰ)求点P的坐标和k的值;
的图像过点P. (Ⅰ)求点P的坐标和k的值;
(Ⅱ)若在这个反比例函数的图像上有两个点(x1 , y1)(x2 , y2),且x1<x2<0,请比较y1与y2的大小.
参考答案:
【答案】解:(Ⅰ)∵△OPQ是边长为 ![]() 的等边三角形, ∴点P的坐标为(
的等边三角形, ∴点P的坐标为( ![]() ,
, ![]() )
)
∵反比例函数的图像过点P,
∴ ![]() =
= ![]() ,
,
解得k= ![]() .
.
(Ⅱ)∵k= ![]() >0,
>0,
在这个反比例函数的图像上有两个点(x1 , y1)(x2 , y2),且x1<x2<0,
∴y1>y2
【解析】(Ⅰ)根据等边三角形的性质得到点P的坐标,根据待定系数法可求k的值;(Ⅱ)由k的值大于0,得到在每一个象限,y随x的增大而减小,利用增减性即可判断.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
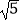 cm,且tan∠EFC=
cm,且tan∠EFC=  ,则矩形ABCD的周长是 .
,则矩形ABCD的周长是 . 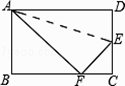
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,点
,点 从点
从点 出发,沿
出发,沿 向点
向点 匀速运动,速度为每秒1个单位,过点
匀速运动,速度为每秒1个单位,过点 作
作 ,交对角线
,交对角线 于点
于点 .点
.点 从点
从点 出发,沿对角线
出发,沿对角线 向点
向点 匀速运动,速度为每秒1个单位.
匀速运动,速度为每秒1个单位.  、
、 两点同时出发,设它们的运动时间为
两点同时出发,设它们的运动时间为 秒(
秒( ).
).(1)当
 时,求出
时,求出 的值;
的值;(2)连接
 ,当
,当 时,求出
时,求出 的值;
的值;(3)试探究:当
 为何值时,
为何值时,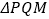 是等腰三角形?
是等腰三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=
 的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y=
的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y= (x>0)的图象交于点D(n,﹣2).
(x>0)的图象交于点D(n,﹣2).(1)k1和k2的值分别是多少?
(2)直线AB,BD分别交x轴于点C,E,若F是y轴上一点,且满足△BDF∽△ACE,求点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学完一元一次方程解法,数学老师出了一道解方程题目:
 .李铭同学的解题步骤如下:
.李铭同学的解题步骤如下:解:去分母,得3(x+1)-2(2-3x)=1;……①
去括号,得3x+3-4-6x=1; ……②
移项,得3x-6x=1-3+4; ……③
合并同类项,得-3x=2; ……④
系数化为1,得x=-
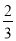 . ……⑤
. ……⑤(1)聪明的你知道李铭的解答过程在第_________(填序号)出现了错误,出现上面错误的原因是违背了____.(填序号)①去括号法则;②等式的性质1;③等式的性质2;④加法交换律.
(2)请你写出正确的解答过程.
-
科目: 来源: 题型:
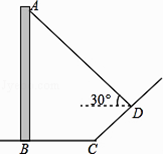
查看答案和解析>>【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,∠AOB、∠COD都是直角.
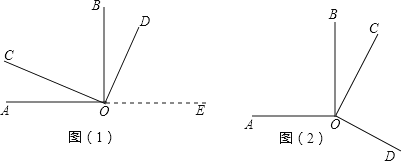
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
相关试题

