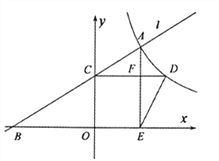
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 的图像上的一个动点,经过点
的图像上的一个动点,经过点![]() 的直线
的直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,交反比例函数的图像于点
轴的垂线,交反比例函数的图像于点![]() .过点
.过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .设点
.设点![]() 的横坐标是
的横坐标是![]() .
.
(1)若![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值,并求出此时直线
的值,并求出此时直线![]() 对应的函数表达式.
对应的函数表达式.
参考答案:
【答案】(1)(![]() a,
a,![]() );(2)y=
);(2)y=![]() x+3.
x+3.
【解析】
(1)由A点坐标可表示出AE的长,利用相似三角形的性质可求得CO的长,代入反比例函数解析式可表示出D点坐标;
(2)由条件可求得D点坐标,由平行四边形的性质可得△ACF∽△ABE,利用相似三角形的性质可求得a的值,则可求得A点坐标,由A、C的坐标,利用待定系数法可求得直线l的函数表达式.
(1)∵点A的横坐标是a,∴点A的纵坐标为![]() ,∴AE=
,∴AE=![]() ,
,
∵AE⊥x轴,∴CO∥AE,∴△BOC∽△BEA,∴![]() =
=![]() =
=![]() ,∴CO=
,∴CO=![]() ,
,
把y=![]() 代入y=
代入y=![]() ,解得x=
,解得x=![]() a,∴D点坐标为(
a,∴D点坐标为(![]() a,
a,![]() );
);
(2)∵OC=3,∴D点纵坐标为3,把y=3代入y=![]() 可得x=4,∴D(4,3),∴CD=4,
可得x=4,∴D(4,3),∴CD=4,
∵四边形BCDE是平行四边形,∴BE=CD=4,且CD∥BE,∴△ACF∽△ABE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得a=2,∴A(2,6),且C(0,3),
,解得a=2,∴A(2,6),且C(0,3),
∴可设直线l的函数表达式为y=kx+3,把x=2,y=6代入,可得6=2k+3,解得k=![]() ,
,
∴直线l的函数表达式为y=![]() x+3.
x+3.
-
科目: 来源: 题型:
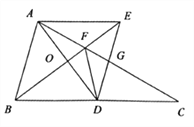
查看答案和解析>>【题目】如图,在
 中,
中, 是
是 边上的中线,
边上的中线,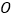 是
是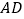 中点,过点
中点,过点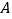 作
作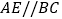 ,交
,交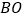 的延长线于点
的延长线于点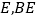 交
交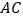 于点
于点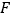 ,连接
,连接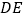 交
交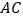 于点
于点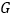 .
.(1)判断四边形
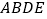 的形状,并说明理由;
的形状,并说明理由;(2)若
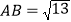 ,且
,且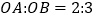 ,求四边形
,求四边形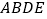 的面积.
的面积.(3)连接
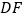 ,求证:
,求证: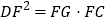 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=2x﹣5与x轴和y轴分别交于点A和点B,抛物线y=﹣x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
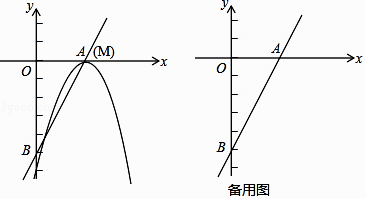
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=﹣x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )
A.3﹣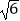 或1+
或1+ 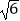
B.3﹣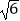 或3+
或3+ 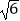
C.3+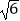 或1﹣
或1﹣ 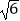
D.1﹣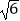 或1+
或1+ 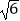
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
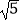 cm,且tan∠EFC=
cm,且tan∠EFC=  ,则矩形ABCD的周长是 .
,则矩形ABCD的周长是 . 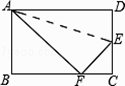
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,点
,点 从点
从点 出发,沿
出发,沿 向点
向点 匀速运动,速度为每秒1个单位,过点
匀速运动,速度为每秒1个单位,过点 作
作 ,交对角线
,交对角线 于点
于点 .点
.点 从点
从点 出发,沿对角线
出发,沿对角线 向点
向点 匀速运动,速度为每秒1个单位.
匀速运动,速度为每秒1个单位.  、
、 两点同时出发,设它们的运动时间为
两点同时出发,设它们的运动时间为 秒(
秒( ).
).(1)当
 时,求出
时,求出 的值;
的值;(2)连接
 ,当
,当 时,求出
时,求出 的值;
的值;(3)试探究:当
 为何值时,
为何值时, 是等腰三角形?
是等腰三角形?

-
科目: 来源: 题型:
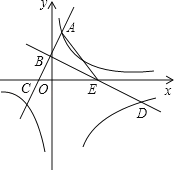
查看答案和解析>>【题目】如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y=
 的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y=
的图象的一个交点为A(1,m),过点B作AB的垂线BD,与反比例函数y= (x>0)的图象交于点D(n,﹣2).
(x>0)的图象交于点D(n,﹣2).(1)k1和k2的值分别是多少?
(2)直线AB,BD分别交x轴于点C,E,若F是y轴上一点,且满足△BDF∽△ACE,求点F的坐标.
相关试题

