【题目】在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:

(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为35°;
(2)在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;
(3)量出A,B两点间的距离为4.5米.
请你根据以上数据求出大树CD的高度.(精确到0.1米)(可能用到的参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
参考答案:
【答案】10.5米
【解析】
试题分析:首先分析图形:本题涉及到两个直角三角形△DBC、△ADC,应利用其公共边CD构造等量关系,借助AB=AD﹣DB=4.5构造方程关系式,进而可求出答案.
解:设CD=x米;
∵∠DBC=45°,
∴DB=CD=x,AD=x+4.5;
在Rt△ACD中,tan∠A=![]() ,
,
∴tan35°=![]() ;
;
解得:x=10.5;
所以大树的高为10.5米.
解法2:在Rt△ACD中,tan∠A=![]() ,∴AD=
,∴AD=![]() ;
;
在Rt△BCD中,tan∠CBD=![]() ,∴BD=
,∴BD=![]() ;
;
而AD﹣BD=4.5,
即![]() ﹣
﹣![]() =4.5,
=4.5,
解得:CD=10.5;
所以大树的高为10.5米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)求方程x2+bx+c=x+m的解.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)3x+5=4x+9
(2)5﹣(x﹣1)=﹣3(x+2)
(3)﹣
 =3x+
=3x+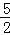
(4)
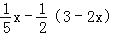 =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
33
48
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
-
科目: 来源: 题型:
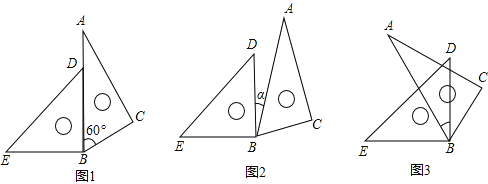
查看答案和解析>>【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在校田径运动会上,小明和其他三名选手参加100米预赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道.若小明首先抽签,则小明抽到1号跑道的概率是( )
A. B. C. D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,如果∠A:∠B:∠C=2:3:5,则按角分,这是一个__三角形.
相关试题

