【题目】直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
(1)求m的值和抛物线的解析式;
(2)求方程x2+bx+c=x+m的解.(直接写出答案)
参考答案:
【答案】(1)m=﹣1,y=x2﹣3x+2;(2)x1=1,x2=3.
【解析】
试题分析:(1)先把A点坐标代入y=x+m可求出m的值,然后把A点和B点坐标代入y=x2+bx+c得到关于b、c的方程组,再解方程方程组求出b、c即可得到抛物线解析式
(2)方程x2+bx+c=x+m的解就是直线y=x+m和抛物线y=x2+bx+c的交点的横坐标.
解:(1)把A(1,0)代入y=x+m得1+m=0,解得m=﹣1,
把A(1,0),B(3,2)代入y=x2+bx+c得![]() ,解得
,解得![]() ,
,
所以抛物线解析式为y=x2﹣3x+2;
(2)方程x2+bx+c=x+m的解为x1=1,x2=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手
表达能力
阅读理解
综合素质
汉字听写
甲
85
78
85
73
乙
73
80
82
83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为给同学们创造更好的读书条件,学校准备新建一个长度为L的度数长廊,并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起,按如图所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.6m.

(1)按图示规律,第一图案的长度L1= m;第二个图案的长度L2= m.
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln之间的关系.
(3)当走廊的长度L为36.6m时,请计算出所需带有花纹图案的瓷砖的块数.
-
科目: 来源: 题型:
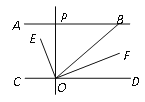
查看答案和解析>>【题目】如下图, AB∥CD, OE平分∠BOC, OF⊥OE, OP⊥CD, ∠ABO=
 a°, 则下列结论:
a°, 则下列结论: ①∠BOE=
 (180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.
(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的个数有多少个? --------------( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)3x+5=4x+9
(2)5﹣(x﹣1)=﹣3(x+2)
(3)﹣
 =3x+
=3x+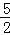
(4)
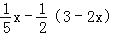 =1.
=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
33
48
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:

(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为35°;
(2)在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;
(3)量出A,B两点间的距离为4.5米.
请你根据以上数据求出大树CD的高度.(精确到0.1米)(可能用到的参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
相关试题

