【题目】如图,在ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连接DE,CF.
BC,连接DE,CF.
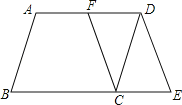
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=10,∠B=60°,求DE的长.
参考答案:
【答案】(1)见详解;(2)![]()
【解析】
(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.
证明:(1)在ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=![]() AD.
AD.
又∵CE=![]() BC,
BC,
∴DF=CE,
∵DF∥CE,
∴四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H.
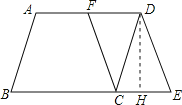
在ABCD中,∵∠B=60°,AD∥BC,
∴∠B=∠DCE,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=![]() CD=2,DH=
CD=2,DH=![]() .
.
在CEDF中,CE=DF=![]() AD=5,则EH=3.
AD=5,则EH=3.
∴在Rt△DHE中,根据勾股定理知
DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a、b、c在数轴上的位置如图所示.

(1)化简:|a|= |b|= ;
(2)比较大小a﹣c 0,a+b 0.
(3)将a,b,c,﹣a,﹣b,﹣c按从小到大的顺序,用“<”号连接.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.
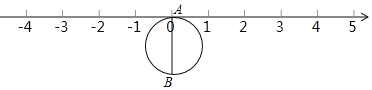
(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3
①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
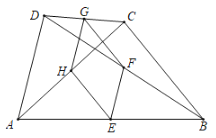
(1)求证:四边形EFGH是平行四边形;
(2)当AD⊥BC时,四边形EFGH是哪种特殊的平行四边形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,运动到3秒钟时,两点相距15个单位长度.已知动点A、B的运动速度比之是3:2(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)A、B两点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
(3)若A、B两点分别从(2)中标出的位置再次同时开始在数轴上运动,运动的速度不变,运动的方向不限,问:经过几秒钟,A、B两点之间相距4个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx的图象过点 (2,0),(-1,6).
(1)求二次函数的关系式;
(2)写出它的对称轴和顶点坐标;
(3)请说明x在什么范围内取值时,函数值y<0?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,m),且与x铀的一个交点在点(3,0)和(4,0)之间,则下列结论:①abc>0;②a﹣b+c>0;③b2=4a(c﹣m);④一元二次方程ax2+bx+c=m+1有两个不相等的实数根,其中正确结论的个数是( )

A.1B.2C.3D.4
相关试题

