【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+
x2+![]() x+2与x轴相交于点A、B,交y轴于点C,抛物线的对称轴交x轴于点N,交线段AC于点M.点F是线段MA上的动点,连接NF,过点N作NG⊥NF交△ABC的边于点G.
x+2与x轴相交于点A、B,交y轴于点C,抛物线的对称轴交x轴于点N,交线段AC于点M.点F是线段MA上的动点,连接NF,过点N作NG⊥NF交△ABC的边于点G.
(1)求证:△ABC是直角三角形;
(2)当点G在边BC上时,连接GF,∠NGF的度数变化吗?若变化,请说明理由;若不变,请求出∠NGF的正切值;
(3)设点F的横坐标为n,点G的纵坐标为m,在整个运动过程中,直接写出m与n的函数关系式,并注明自变量n的取值范围.

参考答案:
【答案】(1)证明见解析;(2)∠NGF的度数不变化,tan∠NGF=![]() ;(3)m与n的关系式为:m=2n–3(
;(3)m与n的关系式为:m=2n–3(![]() ≤n≤
≤n≤![]() )或m=
)或m=![]() (
(![]() <n≤4).
<n≤4).
【解析】(1)先利用抛物线解析式确定A、B、C的坐标,然后利用勾股定理的逆定理进行证明即可;
(2)先利用待定系数法求出直线AC的然后式,则可确定M(![]() ,
,![]() ),再证明△NMF∽△NBG,利用相似比得到
),再证明△NMF∽△NBG,利用相似比得到![]() =
=![]() ,然后根据正切的定义得到tan∠NGF
,然后根据正切的定义得到tan∠NGF![]() ,从而判断∠NGF的度数为定值;
,从而判断∠NGF的度数为定值;
(3)作GH⊥x轴于H,FQ⊥x轴于Q,F(n,–![]() n+2),分点G在BC上,点G在AC上两种情况进行讨论即可得.
n+2),分点G在BC上,点G在AC上两种情况进行讨论即可得.
(1)当x=0时,y=–![]() x2+
x2+![]() x+2=2,则C(0,2);
x+2=2,则C(0,2);
当y=0时,–![]() x2+
x2+![]() x+2=0,解得x1=–1,x2=4,则A(4,0),B(–1,0),(2分)
x+2=0,解得x1=–1,x2=4,则A(4,0),B(–1,0),(2分)
∵BC2=12+22=5,AC2=42+22=20,AB2=25,
∴BC2+AC2=AB2,
∴△ABC为直角三角形,∠ACB=90°;
(2)∠NGF的度数不变化,
设直线AC的解析式为y=kx+b,
把A(4,0),C(0,2)代入得![]() ,解得
,解得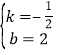 ,
,
∴直线AC的解析式为y=–![]() x+2,
x+2,
∵抛物线的对称轴为直线x=![]() ,∴M(
,∴M(![]() ,
,![]() ),
),
∵GN⊥NF,∴∠GNF=90°,∴∠BNG=∠MNF,
∵∠ACB=90°,∴∠NBC=∠OCA,而MN∥OC,
∴∠NMF=∠OCA,∴∠NBG=∠NMF,∴△NMF∽△NBG,
∴![]() =
=![]() =
=![]() ,∴tan∠NGF=
,∴tan∠NGF=![]() ,
,
∴∠NGF的度数为定值;
(3)作GH⊥x轴于H,FQ⊥x轴于Q,F(n,–![]() n+2),
n+2),
当G点在BC上,如图1,易得直线BC的解析式为y=2x+2,
则G(![]() m–1,m),
m–1,m),
∵∠GNF=90°,∴∠GNH=∠NFQ,∴Rt△NGH∽Rt△FNQ,
∴![]() ,即
,即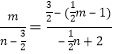 ,
,
∴m=2n–3,
当m=0时,2n–3=0,解得n=![]() ;当m=2时,2n–3=2,解得n=
;当m=2时,2n–3=2,解得n=![]() ;
;
∴此时n的范围为![]() ≤n≤
≤n≤![]() ;
;

当点G在AC上,如图2,则![]() <n≤4,则G(4–2m,m),
<n≤4,则G(4–2m,m),
易得Rt△NGH∽Rt△FNQ,
∴![]() ,即
,即 ,∴m=
,∴m=![]() ,
,
综上所述,故答案为:m与n的关系式为:m=2n–3(![]() ≤n≤
≤n≤![]() )或m=
)或m=![]() (
(![]() <n≤4).
<n≤4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.
(1)尺规作图:①作∠A的平分线,交CB于点D;
②过点D作AB的垂线,垂足为点E.请保留作图痕迹,不写作法,并标明字母.
(2)若AC=3,BC=4,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】第二十四届冬季奥林匹克运动会将与2022年2月20日在北京举行,北京将成为历史上第一座举办过夏奥会又举办过冬奥会的城市,东宝区举办了一次冬奥会知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
(收集数据)
从甲、乙两校各随机抽取20名学生,在这次竞赛中它们的成绩如下:
甲
30
60
60
70
60
80
30
90
100
60
60
100
80
60
70
60
60
90
60
60
乙
80
90
40
60
80
80
90
40
80
50
80
70
70
70
70
60
80
50
80
80
(整理、描述数据)按如下分数段整理、描述这两组样本数据:
(说明:优秀成绩为80<x≤100,良好成绩为50<x≤80,合格成绩为30≤x≤50.)
学校
平均分
中位数
众数
甲
67
60
60
乙
70
75
a
30≤x≤50
50<x≤80
80<x≤100
甲
2
14
4
乙
4
14
2
(分析数据)两组样本数据的平均分、中位数、众数如右表所示:其中a= .
(得出结论)
(1)小伟同学说:“这次竞赛我得了70分,在我们学校排名属中游略偏上!”由表中数据可知小明是 校的学生;(填“甲”或“乙”)
(2)老师从乙校随机抽取一名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为 ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.(至少从两个不同的角度说明推断的合理性)
-
科目: 来源: 题型:
查看答案和解析>>【题目】大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天)
1
2
3
…
50
p(件)
118
116
114
…
20
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+
 .
.(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明(视为小黑点)站在一个高为10米的高台A上,利用旗杆OM顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B.那么小明在荡绳索的过程中离地面的最低点的高度MN是( )

A.2米B.2.2米C.2.5米D.2.7米
-
科目: 来源: 题型:
查看答案和解析>>【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
 (千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与
(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与 之间的函数关系如图所示,折线OAB表示y乙与
之间的函数关系如图所示,折线OAB表示y乙与 之间的函数关系.
之间的函数关系.(1)甲采摘园的门票是 元,在乙园采摘草莓超过______
 后超过部分有打折优惠;
后超过部分有打折优惠;(2)当采摘量
 时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 为
为 的直径,
的直径, 、
、 为
为 的切线,
的切线, 、
、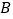 为切点,
为切点,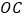 交
交 于点
于点 ,
, 的延长线交
的延长线交 于点
于点 ,连接
,连接 、
、 .给出以下结论:①
.给出以下结论:① ;②
;② ;③点
;③点 为
为 的内心.其中正确的是________(填序号).
的内心.其中正确的是________(填序号).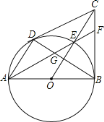
相关试题

