【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与
(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与![]() 之间的函数关系如图所示,折线OAB表示y乙与
之间的函数关系如图所示,折线OAB表示y乙与![]() 之间的函数关系.
之间的函数关系.
(1)甲采摘园的门票是 元,在乙园采摘草莓超过______![]() 后超过部分有打折优惠;
后超过部分有打折优惠;
(2)当采摘量![]() 时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.

参考答案:
【答案】(1)60,30;(2)20千克
【解析】
(1)根据函数图象和图象中的数据可以解答本题;
(2)根据函数图象中的数据可以求得当x>10时,y乙与x的函数表达式及 y甲与x的函数表达式,联立即可求解.
解:(1)由图象可得,
甲采摘园的门票是60元,两个采摘园优惠前的草莓单价是:300÷10=30(元/千克),
故答案为:60,30;
(2)当x>10时,设y乙与x的函数表达式是y乙=kx+b,
![]() ,得
,得![]() ,
,
即当x>10时,y乙与x的函数表达式是y乙=12x+180;
(3)由题意可得,
y甲=60+30×0.6x=18x+60,
当x>10时,令12x+180=18x+60,得x=20,
答:采摘20千克草莓时,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天)
1
2
3
…
50
p(件)
118
116
114
…
20
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+
 .
.(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=
 x2+
x2+ x+2与x轴相交于点A、B,交y轴于点C,抛物线的对称轴交x轴于点N,交线段AC于点M.点F是线段MA上的动点,连接NF,过点N作NG⊥NF交△ABC的边于点G.
x+2与x轴相交于点A、B,交y轴于点C,抛物线的对称轴交x轴于点N,交线段AC于点M.点F是线段MA上的动点,连接NF,过点N作NG⊥NF交△ABC的边于点G.(1)求证:△ABC是直角三角形;
(2)当点G在边BC上时,连接GF,∠NGF的度数变化吗?若变化,请说明理由;若不变,请求出∠NGF的正切值;
(3)设点F的横坐标为n,点G的纵坐标为m,在整个运动过程中,直接写出m与n的函数关系式,并注明自变量n的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明(视为小黑点)站在一个高为10米的高台A上,利用旗杆OM顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B.那么小明在荡绳索的过程中离地面的最低点的高度MN是( )

A.2米B.2.2米C.2.5米D.2.7米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 为
为 的直径,
的直径, 、
、 为
为 的切线,
的切线, 、
、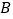 为切点,
为切点,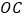 交
交 于点
于点 ,
, 的延长线交
的延长线交 于点
于点 ,连接
,连接 、
、 .给出以下结论:①
.给出以下结论:① ;②
;② ;③点
;③点 为
为 的内心.其中正确的是________(填序号).
的内心.其中正确的是________(填序号).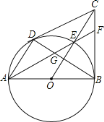
-
科目: 来源: 题型:
查看答案和解析>>【题目】海水养殖是莱州经济产业的亮丽名片之一,某养殖场响应山东省加快新旧动能转换的号召,今年采用新技术投资养殖了200万笼扇贝,并且全部被订购,已知每笼扇贝的成本是40元,售价是100元,打捞出售过程中发现,一部分扇贝生长情况不合要求,最后只能按照25元一笼出售,如果纯收入为
 万元,不合要求的扇贝有
万元,不合要求的扇贝有 万笼.
万笼.(1)求纯收入
 关于
关于 的关系式.
的关系式.(2)当
 为何值时,养殖场不赔不嫌?
为何值时,养殖场不赔不嫌? -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,顶点在格点上的三角形叫做格点三角形,如格点三角形△ABC.
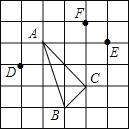
(1)△ABC的面积为 ;
(2)△ABC的形状为 ;
(3)根据图中标示的各点(A、B、C、D、E、F)位置,与△ABC全等的格点三角形是 .
相关试题

