【题目】【问题情境】如图①,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小丽给出的提示是:如图②,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
请根据小丽的提示进行证明.




【变式探究】如图③,当点P在BC延长线上时,其余条件不变,试猜想PD、PE、CF三者之间的数量关系并证明.
【结论运用】如图④,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值.
参考答案:
【答案】见解析;CF=PD+PE ;PG+PH的值为4.
【解析】【问题情境】
分析:【问题情境】连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
【变式探究】连接AP,由△ABP与△ACP面积之差等于△ABC的面积可以证得:CF=PD-PE.
【结论运用】先证BE=BF,过点E作EQ⊥BF,垂足为Q,利用问题情境中的结论可得PG+PH=EQ,易证EQ=DC,故只需求出DC即可.
详解:证明:连接AP,如图②,
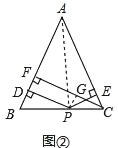
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP+S△ACP,
∴![]() ABCF=
ABCF=![]() ABPD+
ABPD+![]() ACPE.
ACPE.
∵AB=AC,
∴CF=PD+PE.
【变式探究】
证明:连接AP,如图③.
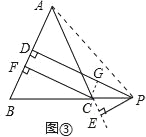
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP﹣S△ACP,
∴![]() ABCF=
ABCF=![]() ABPD﹣
ABPD﹣![]() ACPE.
ACPE.
∵AB=AC,
∴CF=PD﹣PE.
【结论运用】
过点E作EQ⊥BC,垂足为Q,如图④,
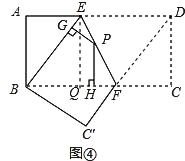
∵四边形ABCD是矩形,
∴AD=BC,∠C=∠ADC=90°.
∵AD=8,CF=3,
∴BF=BC﹣CF=AD﹣CF=5.
由折叠可得:DF=BF,∠BEF=∠DEF.
∴DF=5.
∵∠C=90°,
∴DC=![]() =4.
=4.
∵EQ⊥BC,∠C=∠ADC=90°,
∴∠EQC=90°=∠C=∠ADC,
∴四边形EQCD是矩形,
∴EQ=DC=4.
∵AD∥BC,
∴∠DEF=∠EFB.
∵∠BEF=∠DEF,
∴∠BEF=∠EFB,
∴BE=BF.
由问题情境中的结论可得:PG+PH=EQ,
∴PG+PH=4,
∴PG+PH的值为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下列方式搭建三角形:

(1)填表:
三角形个数
1
2
3
4
…
火柴棒根数
…
(2)当三角形的个数为
 时,火柴棒的根数是多少?
时,火柴棒的根数是多少?(3)求当
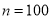 时,有多少根火柴棒?
时,有多少根火柴棒?(4)当火柴棒的根数为2017时,三角形的个数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一边长为36cm的正方形硬纸板进行适当的剪裁,折成一个长方体盒子(纸板的厚度忽略不计)
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.
①要使折成的长方体盒子的底面积为676cm2,那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子,若折成的一个长方体盒子的表面积为880cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程
 (米)与时间
(米)与时间 (分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )
(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )
A.这次比赛的全程是500米
B.乙队先到达终点
C.比赛中两队从出发到1.1分钟时间段,乙队的速度比甲队的速度快
D.乙与甲相遇时乙的速度是375米/分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)你认为图乙中阴影部分的正方形的边长等于多少? .
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;方法二: .
(3)观察图乙,你能写出下列三个代数式之间的等量关系吗?
(m+n)2;(m﹣n)2; mm
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=5,求(a﹣b)2的值.

-
科目: 来源: 题型:
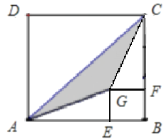
查看答案和解析>>【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.
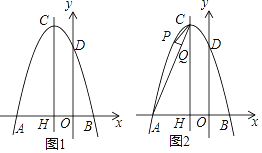
(1)求抛物线的表达式;
(2)点E,F分别是抛物线对称轴CH上的两个动点(点E在点F上方),且EF=1,求使四边形BDEF的周长最小时的点E,F坐标及最小值;
(3)如图2,点P为对称轴左侧,x轴上方的抛物线上的点,PQ⊥AC于点Q,是否存在这样的点P使△PCQ与△ACH相似?若存在请求出点P的坐标,若不存在请说明理由.
相关试题

