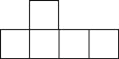
【题目】张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
(1)共有 种弥补方法;
(2)任意画出一种成功的设计图(在图中补充);
(3)在你帮忙设计成功的图中,要把﹣8,10,﹣12,8,﹣10,12这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加得0.(直接在图中填上)
参考答案:
【答案】(1)4;(2)详见解析;(3)详见解析.
【解析】
(1)根据正方体展开图特点:中间4联方,上下各一个,中间3联方,上下各1,2,两个靠一起,不能出“田”字,符合第一种情况,中间四个连在一起,上面一个,下面有四个位置,所以有四种弥补方法;
(2)利用(1)的分析画出图形即可;
(3)想象出折叠后的立方体,把数字填上即可,注意答案不唯一.
解:(1)共有4种弥补方法,
故答案为:4;
(2)如图所示:
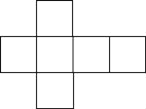 ;
;
(3)如图所示:
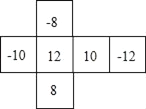 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 两地盛产柑桔,
两地盛产柑桔,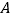 地有柑桔200吨,
地有柑桔200吨,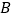 地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知
地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知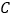 仓库可储存240吨,
仓库可储存240吨,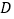 仓库可储存260吨;从
仓库可储存260吨;从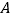 地运往C、D两处的费用分别为每吨20元和25元,从
地运往C、D两处的费用分别为每吨20元和25元,从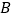 地运往C、D两处的费用分别为每吨15元和18元.设从
地运往C、D两处的费用分别为每吨15元和18元.设从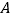 地运往
地运往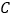 仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.(1)请填写下表后分别求出yA,yB之间的函数关系式,并写出定义域;

C
D
总计
A
x吨
200吨
B
300吨
总计
240吨
260吨
500吨
(2)试讨论A,B两地中,哪个运费较少;
-
科目: 来源: 题型:
查看答案和解析>>【题目】“国庆节大酬宾”,某商场设计的促销活动如下:在一个不透明的箱子里放有3个质地相同的小球,并在球上分别标有“5元”、“10元”和“15元”的字样,规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两个小球所标金额和返还相等价格的购物券,购物券可以在本商场消费,某顾客刚好消费300元.
(1)该顾客最多可得到元购物券;
(2)请你用画树状图和列表的方法,求出该顾客所得购物券的金额不低于25元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD的边长为
 厘米,对角线AC上的两个动点E,F,点E从点A、点F从点C同时出发,沿对角线以1厘米/秒的相同速度运动,过E作EH⊥AC交Rt△ACD的直角边于H;过F作FG⊥AC交Rt△ACD的直角边于G,连接HG,EB.设HE,EF,FG,GH围成的图形面积为
厘米,对角线AC上的两个动点E,F,点E从点A、点F从点C同时出发,沿对角线以1厘米/秒的相同速度运动,过E作EH⊥AC交Rt△ACD的直角边于H;过F作FG⊥AC交Rt△ACD的直角边于G,连接HG,EB.设HE,EF,FG,GH围成的图形面积为 ,AE,EB,BA围成的图形面积为
,AE,EB,BA围成的图形面积为 (这里规定:线段的面积为
(这里规定:线段的面积为 ).E到达C,F到达A停止.若E的运动时间为x秒,解答下列问题:
).E到达C,F到达A停止.若E的运动时间为x秒,解答下列问题:(1)如图①,判断四边形EFGH是什么四边形,并证明;
(2)当0<x<8时,求x为何值时,
 ;
;(3)若
 是
是 的和,试用x的代数式表示y.(图②为备用图)
的和,试用x的代数式表示y.(图②为备用图)

-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图示的对话解答下列问题.

求:(1)a,b的值;
(2)8﹣a+b﹣c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式a=
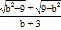 +2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
+2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )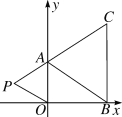
A. (-3,1) B. (-2,1) C. (-4,1) D. (-2.5,1)
-
科目: 来源: 题型:
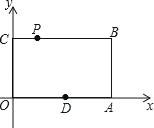
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是_____.
相关试题

