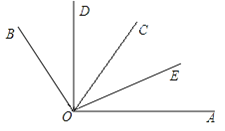
【题目】已知:如图所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)求出∠DOC和∠AOE的度数,并判断∠DOE 与∠AOB是否互补,并说明理由;
(3)若∠BOC=α,∠AOC=β,则∠DOE 与∠AOB是否互补,并说明理由.
参考答案:
【答案】(1)∠AOB=120°,其补角为60°;(2)∠DOE=60°,∠AOB=120°,∠DOE与∠AOB互补;(3)∠DOE与∠AOB不互补,理由见解析.
【解析】
(1)由∠AOB=∠BOC+∠AOC,以及补角的定义,即可得到答案;
(2)根据角平分线的定义,即可求出∠DOE和∠AOE的度数,然后∠DOE+∠AOB=180°,即可得到答案;
(3)分别求出∠DOE与∠AOB的度数,然后进行判断,即可得到答案.
解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
其补角为:180°![]() ∠AOB=180°
∠AOB=180°![]() 120°=60°.
120°=60°.
(2)∠DOE与∠AOB互补;
理由如下:∵OD平分∠BOC,OE平分∠AOC,
∴∠DOC=![]() ∠BOC=
∠BOC=![]() ×70°=35°,∠COE=
×70°=35°,∠COE=![]() ∠AOC=
∠AOC=![]() ×50°=25°.
×50°=25°.
∴∠DOE=∠DOC+∠COE =35°+25°=60°.
∴∠DOE+∠AOB=60°+120°=180°,
∴∠DOE与∠AOB互补.
(3)∠DOE与∠AOB不互补,
理由如下:∵OD平分∠BOC,OE平分∠AOC,
∴∠DOC=![]() ∠BOC=
∠BOC=![]() α,∠COE=
α,∠COE=![]() ∠AOC=
∠AOC=![]() β.
β.
∴∠DOE=∠DOC+∠COE =![]() α+
α+![]() β=
β=![]() (α+β).
(α+β).
∴∠DOE+∠AOB=![]() (α+β)+(α+β)=
(α+β)+(α+β)=![]() (α+β),
(α+β),
∴∠DOE与∠AOB不互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我乡某校举行全体学生“定点投篮”比赛,每位学生投40个,随机抽取了部分学生的投篮结果,并绘制成如下统计图表。
组别
投进个数
人数
A

10
B

15
C
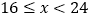
30
D
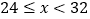
m
E

n
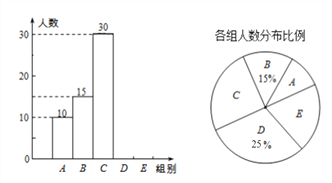
根据以上信息完成下列问题。
①本次抽取的学生人数为多少?
②统计表中的m=__________;
③扇形统计图中E组所占的百分比;
④补全频数分布直方图;
⑤扇形统计图中“C组”所对应的圆心角的度数;
⑥本次比赛中投篮个数的中位数落在哪一组;
⑦已知该校共有900名学生,如投进个数少于24个定为不合格,请你估计该校本次投篮比赛不合格的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形的是( )
A. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/27/1911053122682880/1914886922772480/STEM/c8503fddf66f4b8c93035a98d8f9f214.png] B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球
两红
一红一白
两白
礼金券(元)
18
24
18
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】防洪大堤的横截面如图所示,已知AE∥BC,背水坡AB的坡度
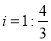 ,且AB=20米.身高1.7米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度为( )
,且AB=20米.身高1.7米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
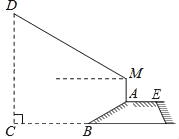
A. 30米 B. 32米 C. 34米 D. 36米
-
科目: 来源: 题型:
查看答案和解析>>【题目】王达和李力是八(2)班运动素质最好的两位同学,为了选出一名同学参加全校的体育运动大寒,班主任针对学校要测试的五个项目,对两位同学进行相应的测试(成绩:分),结果如下:
姓名
力量
速度
耐力
柔韧
灵敏
王达
60
75
100
90
75
李力
70
90
80
80
80
根据以上测试结果解答下列问题:
(1)补充完成下表:
姓名
平均成绩(分)
中位数(分)
众数(分)
方差(分2)
王达
80
75
75
190
李力
(2)任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由;
(3)若按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,推选得分同学参加比赛,请通过计算说明应推选哪位同学去参赛。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蛋糕店为了吸引顾客,在A、B两种蛋糕中,轮流降低其中一种蛋糕价格,这样形成两种盈利模式,模式一:A种蛋糕利润每盒8元,B种蛋糕利润每盒15元;模式二:A种蛋糕利润每盒14元,B种蛋糕利润每盒11元每天限定销售A、B两种蛋糕共40盒,且都能售完,设每天销售A种蛋糕x盒
(1)设按模式一销售A、B两种蛋糕所获利润为y1元,按模式二销售A、B两种蛋糕所获利润为y2元,分别求出y1、y2关于x的函数解析式;
(2)在同一个坐标系内分别画出(1)题中的两个函数的图象;

(3)若y始终表示y1、y2中较大的值,请问y是否为x的函数,并说说你的理由,并直接写出y的最小值.
相关试题

