【题目】我乡某校举行全体学生“定点投篮”比赛,每位学生投40个,随机抽取了部分学生的投篮结果,并绘制成如下统计图表。
组别 | 投进个数 | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 30 |
D |
| m |
E |
| n |
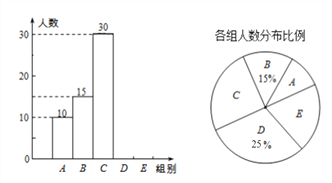
根据以上信息完成下列问题。
①本次抽取的学生人数为多少?
②统计表中的m=__________;
③扇形统计图中E组所占的百分比;
④补全频数分布直方图;
⑤扇形统计图中“C组”所对应的圆心角的度数;
⑥本次比赛中投篮个数的中位数落在哪一组;
⑦已知该校共有900名学生,如投进个数少于24个定为不合格,请你估计该校本次投篮比赛不合格的学生人数.
参考答案:
【答案】①100; ②25;③20%;④见解析;⑤108;⑥C;⑦该校本次投篮比赛不合格的学生人数495人。
【解析】分析:(1)根据B组有15人,所占的百分比是15%即可求得总人数;
(2)用(1)中求得的总人数×D所占的百分比求解;
(3)利用360度乘以对应的比例即可求解;
(4)利用(1)中求得的总人数乘以对应的比例即可求解D和E组的人数.
详解:①15÷15%=100;
②m=100×25%= 25;
③(100-10-15-30-25)÷100= 20%;
④D组人数为25,E组人数为20,如图;
⑤![]() ;
;
⑥∵第50和51名都落在C组;
∴本次比赛中投篮个数的中位数落在C 组;
⑦![]() 人,
人,
答:该校本次投篮比赛不合格的学生人数495人。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

-
科目: 来源: 题型:
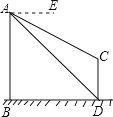
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数,合数等,现在我们来研究另一种特珠的自然数“纯数”.
定义:对于自然数
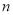 ,在计算
,在计算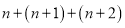 时,各数位都不产生进位,则称这个自然数
时,各数位都不产生进位,则称这个自然数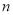 为“纯数”,例如:32是“纯数”,因为计算
为“纯数”,例如:32是“纯数”,因为计算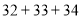 时,各数位都不产生进位;23不是“纯数”,因为计算
时,各数位都不产生进位;23不是“纯数”,因为计算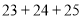 时,个位产生了进位.
时,个位产生了进位.(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形的是( )
A. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/27/1911053122682880/1914886922772480/STEM/c8503fddf66f4b8c93035a98d8f9f214.png] B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球
两红
一红一白
两白
礼金券(元)
18
24
18
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
-
科目: 来源: 题型:
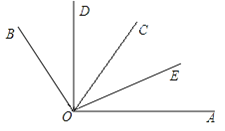
查看答案和解析>>【题目】已知:如图所示,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)求出∠DOC和∠AOE的度数,并判断∠DOE 与∠AOB是否互补,并说明理由;
(3)若∠BOC=α,∠AOC=β,则∠DOE 与∠AOB是否互补,并说明理由.
相关试题

