搜索
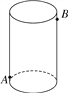
【题目】如图，圆柱形玻璃容器高19cm，底面周长为60cm，在外侧距下底1.5cm的点A处有一只蜘蛛，在蜘蛛正对面的圆柱形容器的外侧，距上底1.5cm处的点B处有一只苍蝇，蜘蛛急于捕捉苍蝇充饥，请你帮蜘蛛计算它沿容器侧面爬行的最短距离．
参考答案：
【答案】蜘蛛沿容器侧面爬行的最短距离为34cm.
【解析】试题分析：将圆柱侧面展开成长方形MNQP，过点B作BC⊥MN于点C，连接AB，线段AB的长度即为所求的最短距离,利用勾股定理进行运算即可.
试题解析：如图，将圆柱侧面展开成长方形MNQP，过点B作BC⊥MN于点C，连接AB，
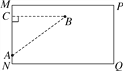
则线段AB的长度即为所求的最短距离．
在Rt△ACB中，AC＝MN－AN－CM＝16cm，
BC是上底面的半圆周的长，即BC＝30cm.
由勾股定理，得AB2＝AC2＋BC2＝162＋302＝1156＝342，
所以AB＝34cm.
故蜘蛛沿容器侧面爬行的最短距离为34cm.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图．电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A，B，C都可使小灯泡发光．
（1）任意闭合其中一个开关，则小灯泡发光的概率等于；
（2）任意闭合其中两个开关，请用画树状图或列表的方法求出小灯泡发光的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠A＝∠F，∠C＝∠D， 根据图形填空，并在括号内注明理由.
解：∵∠A＝∠F
∴AC∥________(内错角相等，两直线平行）
∴∠1 ＝∠D（_________________________________)
∵∠C ＝∠D（已知）
∴∠1＝___________（等量代换）
∴BD∥___________（________________________________）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB＝10，AC＝2
，BC边上的高AD＝6，则另一边BC等于_______．【答案】10或6
【解析】试题解析：根据题意画出图形，如图所示，
如图1所示，AB=10，AC=2
，AD=6，在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD=
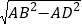=8，CD=
=2，此时BC=BD+CD=8+2=10；
如图2所示，AB=10，AC=2
，AD=6，在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD=
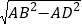=8，CD==2，此时BC=BD-CD=8-2=6，
则BC的长为6或10．
【题型】填空题
【结束】
12【题目】在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1 ______ y2．（填“＞”“＜”或“=”）
-
科目： 来源： 题型：
查看答案和解析>>【题目】旅客乘车按规定可以随身携带一定重量的行李，如果超过规定，则需要购买行李票，设行李费y（元）与行李重量x(千克)的关系如图，根据图象回答下列问题：
（1）行李重量在________千克以内，不必交费;
（2）当行李重量60千克时，交费____元;
（3）当行李重量________千克时，交费10元;
（4）行李重量每增加1千克，多交_________元;
（5）y= __________ ( y与x之间的关系式)
-
科目： 来源： 题型：
查看答案和解析>>【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注，人工智能完胜李世石．某教学网站开设了有关人工智能的课程并策划了A，B两种网上学习的月收费方式：
收费
方式
月使用费(元)
包时上网
时间(h)
超时费(元/min)
A
7
25
0.6
B
10
50
0.8
设小明每月上网学习人工智能课程的时间为x小时，方案A，B的收费金额分别为yA元，yB元．
(1)当x≥50时，分别求出yA，yB与x之间的函数关系式；
(2)若小明3月份上该网站学习的时间为60小时，则他选择哪种方式上网学习合算？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB为半圆直径，O为圆心，C为半圆上一点，E是弧AC的中点，OE交弦AC于点D，若AC=8cm，DE=2cm，求OD的长．
相关试题
