【题目】如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.

参考答案:
【答案】(1) 桥拱的半径为50 m;(2)这艘轮船能顺利通过,理由见解析.
【解析】试题分析:
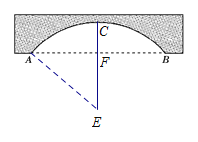
(1)找到圆的圆心E,过点E作EF⊥AB于点F,延长EF交![]() 于点C,连接AE,在Rt△AEF中用勾股定理求AE的长;
于点C,连接AE,在Rt△AEF中用勾股定理求AE的长;
(2)连接EM,设EC与MN的交点为D,在Rt△DME中,用勾股定理求出DE,再求DF的长,比较DF与9的大小,即可求解.
试题解析:
(1)如图,点E是桥拱所在圆的圆心.过点E作EF⊥AB于点F,
延长EF交![]() 于点C,连接AE,则CF=20 m.由垂径定理知,F是AB的中点,
于点C,连接AE,则CF=20 m.由垂径定理知,F是AB的中点,
∴AF=FB=![]() AB=40 m.设半径是r m,由勾股定理,得AE2=AF2+EF2=AF2+(CE-CF)2,即r2=402+(r-20)2.解得r=50.∴桥拱的半径为50 m.
AB=40 m.设半径是r m,由勾股定理,得AE2=AF2+EF2=AF2+(CE-CF)2,即r2=402+(r-20)2.解得r=50.∴桥拱的半径为50 m.
(2)这艘轮船能顺利通过.理由如下:
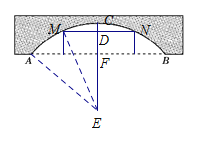
当宽60 m的轮船刚好可通过拱桥时,如图,MN为轮船顶部的位置.
连接EM,设EC与MN的交点为D,
则DE⊥MN,∴DM=30 m,∴DE=![]() =
=![]() =40(m).
=40(m).
∵EF=EC-CF=50-20=30(m),∴DF=DE-EF=40-30=10(m).
∵10 m>9 m,∴这艘轮船能顺利通过.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明调查了全班本学期阅读课外书的情况,并根据统计数据,绘制如下的频率分布折线图和扇形统计图。
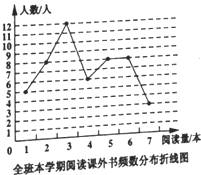
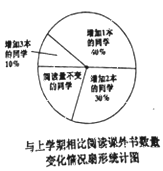
根据以上信息,回答下列问题:
①这个班共有__________ 名学生,本学期阅读量5本的有________ 人
②这个班本学期阅读量的中位数是_______ 本,众数是 ______ 本;
③求全班本学期比上学期每名同学的平均阅读量增加了多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形填写下表:
链条节数(节)
2
3
4
链条长度(cm)
(2)如果x节链条的总长度是y,求y与x之间的关系式;
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧
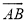 围成的弓形面积.
围成的弓形面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是x=
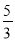 .
.(1)求这条抛物线的关系式.
(2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有5个边长为1的小正方形组成的纸片,可以把它剪拼成一个正方形.
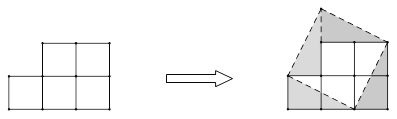
(1) 拼成的正方形的面积是 ,边长是 ;
(2) 在数轴上作出表示
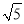 、-2
、-2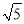 的点;
的点;(3) 你能把这十个小正方形组成的图形纸,剪开并拼成一个大正方形吗?若能,在图中画出拼接后的正方形,并求边长,若不能,请说明理由.

相关试题

