搜索
【题目】已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是x=
.
(1)求这条抛物线的关系式.
(2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.
参考答案：
【答案】（1）y=
.（2）证明见解析.
【解析】本题主要考查了抛物线与x轴的交点和待定系数法求二次函数解析式
（1）先设出函数的解析式：y=ax2+bx+c，根据抛物线经过A（0，3），B（4，6）两点，用待定系数法求出函数的解析式；
（2）令y=0，得到方程，根据方程根与系数的关系求出抛物线与x轴的两个交点，再根据三角形任意两边之和大于第三边，来证明．
(1)解:设所求抛物线的关系式为y=ax2+bx+c,
∵A(0,3),B(4,6),对称轴是直线x=
.
∴
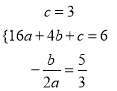, 解得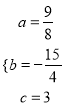
∴y=
.
(2)证明:令y=0,得
="0," ∴
∵A(0,3),取A点关于x轴的对称点E,∴E (0,-3).
设直线BE的关系式为y=kx-3,把B(4,6)代入上式,得6=4k-3,
∴k=
,∴y=
x-3 .
由
x-3=0,得x=
.
故C为
,C点与抛物线在x轴上的一个交点重合,
在x轴上任取一点D,在△BED中,BE< BD+DE.
又∵BE=EC+BC,EC=AC,ED=AD,∴AC+BC<AD+BD.
若D与C重合,则AC+BC="AD+BD." ∴AC+BC≤AD+BD.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧
围成的弓形面积. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一拱形公路桥，圆弧形桥拱的水面跨度AB＝80 m，桥拱到水面的最大高度为20 m.(1)求桥拱的半径．
(2)现有一艘宽60 m，顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥，这艘轮船能顺利通过吗？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，有5个边长为1的小正方形组成的纸片，可以把它剪拼成一个正方形.
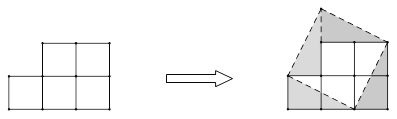
(1) 拼成的正方形的面积是 ，边长是 ；
(2) 在数轴上作出表示
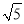、-2
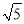的点；(3) 你能把这十个小正方形组成的图形纸，剪开并拼成一个大正方形吗？若能，在图中画出拼接后的正方形，并求边长，若不能，请说明理由.
-
科目： 来源： 题型：
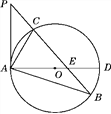
查看答案和解析>>【题目】如图，已知在△ABP中，C是BP边上一点，∠PAC＝∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E.(1)求证：PA是⊙O的切线；
(2)过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG·AB＝12，求AC的长；(3)在满足(2)的条件下，若AF∶FD＝1∶2，GF＝1，求⊙O的半径及sin∠ACE的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知下表:
x
0
1
2
ax2
1
ax2+bx+c
3
3
(1)求a、b、c的值，并在表内空格处填入正确的数；
(2)请你根据上面的结果判断:
①是否存在实数x,使二次三项式ax2+bx+c的值为0?若存在,求出这个实数值;若不存在,请说明理由.
②画出函数y=ax2+bx+c的图象示意图,由图象确定,当x取什么实数时,ax2+ bx+c>0?
相关试题
